こんにちは、かじつとむです。
みなさんは確率というものをご存知でしょうか?
中学・高校のときに学んだ確率ですが、データ分析や統計学を学ぶ上では非常に重要な考え方になります。
たとえば、統計学を用いたデータ分析には、何%の確率で〇〇〜△△の値の間に存在する、といった具合に確率は使われます。
今回は、そんな確率について概要から計算方法まで解説します。
この記事を読んで以下のことがわかります。
- 確率について理解できる
- 確率の計算方法について理解できる
それではいってみましょう!
統計学に必要な確率について:確率とは

確率とは、ある現象(事象)の起こりやすさの度合いのことです。
宝くじを例にとって説明しますと、宝くじのあたりやすさや、その反対のハズレやすさが確率となります。
では、確率の式について説明します。
ある現象Aが起こる確率をP(A)と表現します。このPは確率を英単語probabilityの頭文字の意味です。
確率P(A)の式は以下のようになります。
$$ P(A) = \frac{現象Aが起こる場合の数}{起こりうるすべての場合の数} $$
ここでいう場合の数とは、ある現象が起こるすべての場合の総数をさします。
起こりうるすべての場合の数を数えるときに注意点があります。
それは「同様に確からしい」ものを数えるということです。
同様に確からしいとは、起こる可能性の割合が同じであることをいいます。
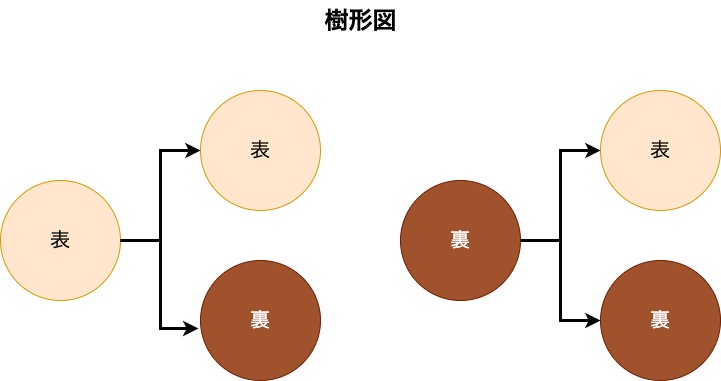
たとえば、コインを1枚投げる場合の起こる現象は、表が出るか、裏が出るかになります。
このとき、表が出ることも、裏が出ることも起こる可能性は同じであることがわかります。
これが同様に確からしいという意味になります。
次に具体的な確率の計算方法について説明します。
統計学に必要な確率について:確率の求め方
たとえば、くじ引きについて以下のような問題を考えてみましょう。
5本のくじの中に当たりが2本入っています。A、Bの順にくじを引きました。
一度引いたくじはもとに戻さないとき、Bが当たりを引く確率はいくつか?
この確率を計算するのに必要なのは、くじ引きで起こりうるすべての場合の数と、Bが当たりを引く場合の数です。先ほどの確率の式を用いて表すと以下のようになります。
$$ P(Bが当たり) = \frac{Bが当たりを引く場合の数}{くじ引きで起こりうるすべての場合の数} $$
この2つの場合の数を数えればBが当たりを引く確率を計算できます。
では、どのようにすれば場合の数を数えることができるようになるのでしょうか?
一番簡単な方法は樹形図を用いて場合の数を数えることです。
樹形図とは、ものごとを順番に書き出して数える方法です。
くじ引きで樹形図を作成すると以下のようになります。
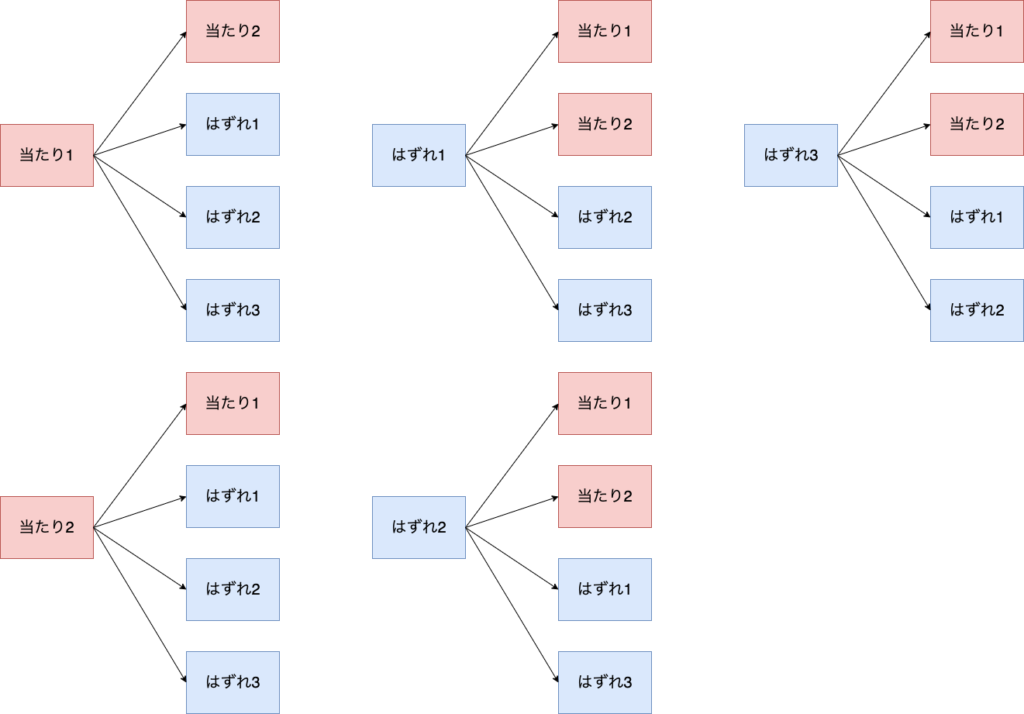
ここで、重要なのはくじ1本1本を区別して数えることです。
たとえば、当たりが2本ある場合、当たり1、当たり2といったようにすべて異なるものとして考えます。
このようにすることでそれぞれのくじ1本1本を引く割合が同じになります。すなわち、くじ引きの場合の数を数える上で同様に確からしい状態にすることができます。
樹形図の数を数えると、くじ引きで起こりうるすべての場合の数は20通りであることがわかります。
次に、この樹形図を使ってBが当たりを引く場合の数を数えていきたいと思います。
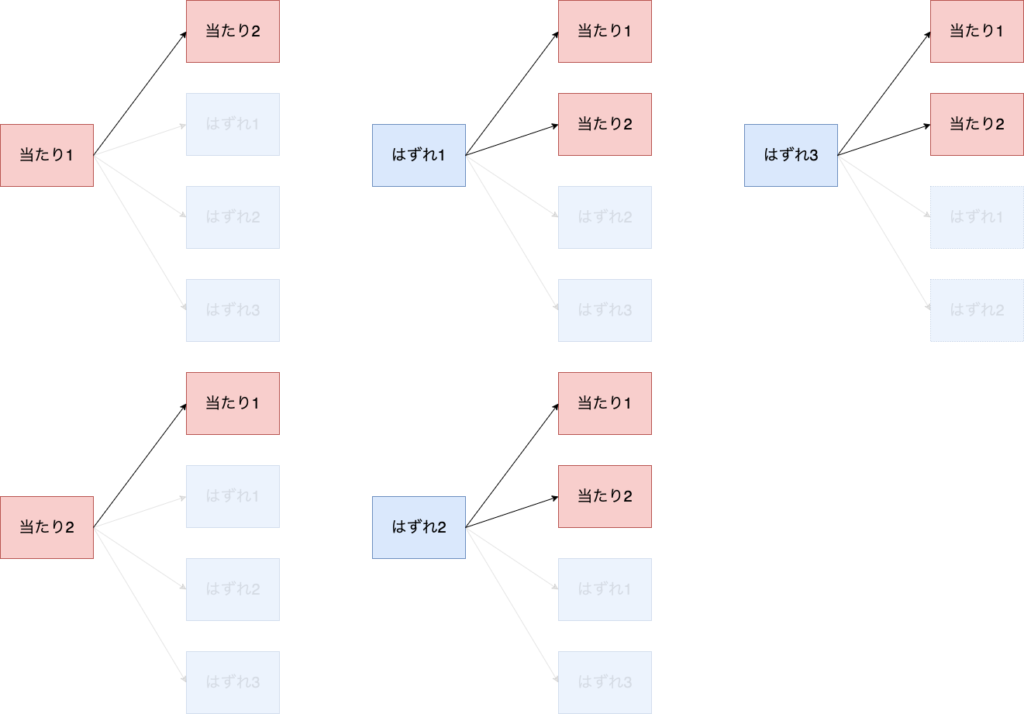
Bが当たりを引く場合の数は、2番目に当たりがあるものを数えれば良いということになります。
上の樹形図より、2番目に当たりがあるものは8個ありますのでBが当たりを引く場合の数は8通りということになります。
最後に、くじ引きで起こりうるすべての場合の数:20通りとBが当たりを引く場合の数:8通りを確率の式に当てはめます。
$$ P(Bが当たる) = \frac{Bが当たりを引く場合の数}{くじ引きで起こりうるすべての場合の数} = \frac{8}{20} = \frac{2}{5} $$
確率を計算するには、Bが当たりを引く場合の数をくじ引きで起こりうるすべての場合の数で割れば良いということになります。
結果、Bが当たる確率は2/5となります。
ここで、Bが当たる確率2/5について考えていきたいと思います。
まず、この問題においてAが当たる確率は次のように計算できます。
$$ P(Aが当たる) = \frac{Aが当たりを引く場合の数}{くじ引きで起こりうるすべての場合の数} = \frac{2}{5} $$
Aは一番はじめにくじを引きますので、くじ引きで起こりうるすべての場合の数は5通りとなります。
そして、Aが当たりを引く場合の数は当たりの数そのものになりますので2通りです。
これらを確率の式に当てはめますと2/5となります。
つまり、Aが当たりを引く確率もBが当たりを引く確率も同じ2/5になったことがわかります。
また計算過程は省略しますが、追加でCが3番目に、Dが4番目に、Eが最後にくじを引いても、くじが当たる確率は同じ2/5となります。
すなわち、くじ引きにおいては先にくじを引こうが、後にくじを引こうが同じ確率になるということがなんとなく想像できるのではないかと思います。
ではより膨大で複雑な場合の数を数えるにはどのようにすれば良いのでしょうか?
その答えは順列や組み合わせを使って場合の数を計算することです。
順列や組み合わせを使った計算方法については以下の記事をご参照ください!
統計学に必要な確率について:まとめ
いかがでしたでしょうか?以下まとめです。
- 確率とは、ある現象の起こりやすさの度合いのことである
- 確率を計算するには、すべての起こりうる場合の数と現象が起こる場合の数を数える必要がある
- 場合の数を数える場合、同様に確からしいものを数える必要がある
- 場合の数を数える方法として、ものごとを順番に書き出す樹形図がある
みなさんもぜひ身近なものの確率について考えてみてください。
最後までこの記事を読んでいただきありがとうございます。
統計学に必要な数学を勉強したい方へ
統計学に使うような確率の基礎知識について勉強したい方は「ふたたびの確率・統計[1]確率編」がおすすめです。
この本は、統計学に必要な集合や場合の数、確率について理解するのにおすすめの書籍となります。
集合や場合の数、確率についてはわかりやすく、かつ、数学的なきごうについても網羅的に学ぶことができます。
本の巻末には、大学入試問題を使った腕試しもできるので、高校生にとってもおすすめの書籍となります。
数学の用語等も図解でわかりやすく、かつ丁寧に解説しておりますので、中学や高校生のときに数学が苦手だった方でもとっつきやすい本となります。
もしこの本で勉強したい方がいれば、ぜひ以下のリンクからどうぞ!
みなさんもぜひ確率について勉強してみましょう!
最後までこの記事を読んでいただきありがとうございました!
統計学やデータサイエンスについて動画で勉強したい方はこちら
![]()






コメント