こんにちは、かじつとむです。
前回は母分散がわかっているときの母平均の区間推定をする方法について説明しました。
今回は母分散がわかっていないときの母平均の区間推定をする方法について説明します。
この記事を読むことで以下のことがわかります。
- 母分散がわかっていない場合の母平均の区間推定方法について理解できる
- 母分散がわかっていない場合の区間推定で使われる、t分布と自由度について理解できる
それでは、いってみましょう!
母平均を推定する区間推定(母分散がわからない場合):結論
母分散がわかっていない場合、母平均を区間推定する方法は以下の通りです。

母分散がわかっていない場合、標本平均$\bar{X}$、標本の数$n$、標本から得られる不偏分散$U^2$という統計量とt分布を用いて母平均の信頼区間を算出します。
不偏分散は、標本から得られるデータより以下の式で計算することができます。
$$ 不偏分散:U^2 = \frac{(標本のデータと標本平均の差)^2の合計}{標本の数-1} $$
不偏分散は、標本分散と少しだけ違い、割る数が標本の数から1引いたもので割るという特徴があります。
不偏分散や標本分散の違いについては、点推定の記事で説明していますのでこちらをご参照ください。
今回新しく出てきた言葉としてt分布があります。
t分布とは、自由度$m$によって変化する確率分布です。
しかし、そもそも自由度mがわからない可能性がありますので、まずは自由度の解説をします。
母平均を推定する区間推定(母分散がわからない場合):自由度とは
自由度とは、自由に決めることができる値の数のことをいいます。
標本では、自由度は標本の数$n$から1を引くことであらわすことができる値となります。
$$ 自由度:m = n – 1 $$
なぜ、標本の数から1を引くことで自由度をあらわすことができるのでしょうか?
答えは、標本平均が決まり、1つの標本以外の値を自由に決められる場合、残り1つの標本は強制的に決まってしまうからです。
少しわかりづらいと思いますので、以下の具体例で考えてみましょう!
A、B、Cの3人の平均身長が170cmである。
このとき、標本はAの身長、Bの身長、Cの身長となり、標本の数は3となります。
また、平均身長が170cmと決まっているため、標本平均も170cmとなります。
数式にすると、以下のようになります。

ここで、Aの身長を160cm、Bの身長を180cmと任意で決めた場合、Cの身長は170cmと強制的に決まります。
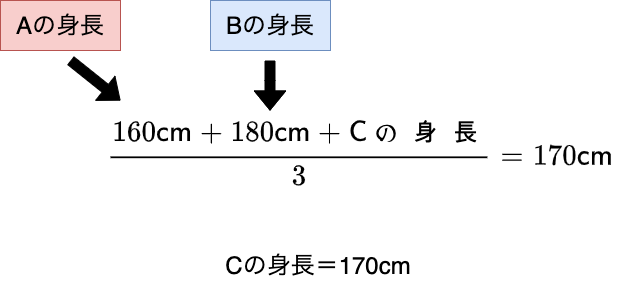
このように、標本の3つの中で2つの値を自由に決めることで残り1つの値は強制的に決まります。
この自由に決めることができる値の数が自由度となります。
この例より標本の数を$n$として考えると、標本の1つ以外は自由に決めることができるため、自由度は$n-1$となります。
自由度がわかったところで、次はその自由度によって決まる確率分布、t分布について説明します。
母平均を推定する区間推定(母分散がわからない場合):t分布とは
t分布とは、平均値を1の標準正規分布のような分布です。
しかし、標準正規分布よりも分布の広がり具合が大きいのが特徴です。
t分布は自由度によって分布の形が異なります。
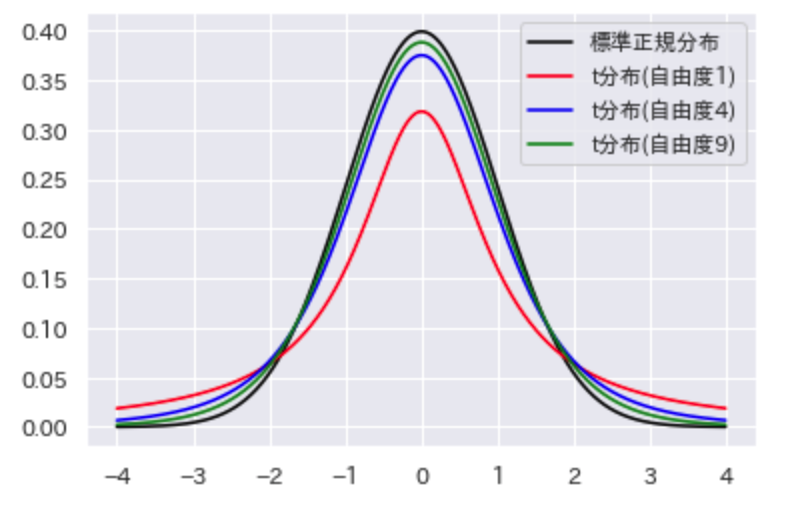
t分布は、自由度が大きければ大きいほど、分布の広がり方が小さくなります。
自由度が$\infty$になるとt分布は標準正規分布となります。
t分布で母平均を区間推定するには、統計量$t$を計算する必要があります。
統計量$t$は標本平均$\bar{X}$、標本の数$n$、不偏分散$U^2$、そして、母平均$\mu$を用いて以下のようにあらわします。
$$ t = \frac{\bar{X}-\mu}{\sqrt{\frac{U^2}{n}}} $$
この$t$に対して、どのくらいの信頼区間で推定したいのかによって区間推定をしていきます。
では、どのように母平均の区間推定をしていくか、具体例を使って説明します。
母平均を推定する区間推定(母分散がわからない場合):区間推定の手順
母分散がわかっていない場合の母平均の区間推定の手順について以下にまとめます。
- 推定したい標本に対して、標本平均と不偏分散を算出する
- 標本平均、標本の数、不偏分散、母平均$\mu$を用いて、統計量$t$を算出する
- 求めたい信頼区間(何パーセントの精度)と自由度から統計量$t$の信頼区間を形成する
- 統計量$t$の信頼区間を母平均$\mu$であらわす
この手順を、以下の例に当てはめながら計算していきましょう!
成人男性10人の身長のデータから、成人男性全体の身長の母平均を区間推定したい。
ただし、母平均がわかっていないものであり、信頼区間は95%とする。
成人男性の身長のデータは以下にあらわす。
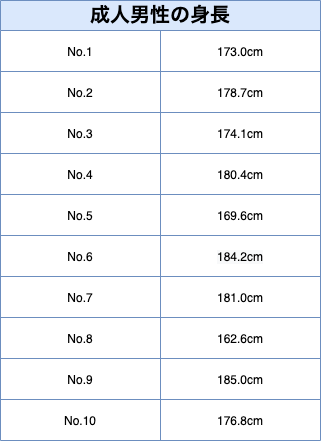
母平均を推定する区間推定(母分散がわからない場合)の手順 その1:標本平均と不偏分散の算出
標本のデータから、標本平均を算出します。
標本平均$\bar{X}$は以下のように算出します。
$$ 標本平均:\bar{X} = \frac{データの合計}{データの数} = \frac{173.0+178.7+\cdots+176.8}{10} = 176.54 $$
また、標本平均を使って不偏分散$U^2$を算出します。
$$ 不偏分散:U^2 = \frac{(標本のデータと標本平均の差)^2の合計}{標本の数-1} $$ $$ = \frac{(173.0 – 176.54)^2 + (178.7-176.54)^2 + \cdots + (176.8-176.54)^2}{10 – 1} = 47.86 $$
よって、標本平均は176.54、不偏分散は47.86を算出することができました。
母平均を推定する区間推定(母分散がわからない場合)の手順 その2:統計量$t$の算出
次に、統計量$t$を算出します。
統計量$t$は、標本平均:176.54、標本の数:10、不偏分散:47.86、そして、母平均$\mu$を用いて以下のようにあらわします。
$$ 統計量:t = \frac{176.54-\mu}{\sqrt{\frac{47.86}{10}}} $$
以上のように、統計量$t$を母平均$\mu$であらわすことができました。
母平均を推定する区間推定(母分散がわからない場合)の手順 その3:統計量$t$の信頼区間の形成
次に統計量$t$の信頼区間を形成します。
まず、求めたい信頼区間を決めます。
たとえば、90%の範囲で推定したいのか、95%の範囲で推定したいのか、99%の範囲で推定したいのかを決めます。
一般的に区間推定を行う場合の信頼区間は95%といわれています。また今回の例も信頼区間は95%としているので、これを用いましょう。
次に自由度:$m$を確認します。自由度は標本の数から1を引いた数になります。
今回の標本の数は10であることから自由度は9となります。
$$ 自由度:m = n-1 = 10-1 =9 $$
求めたい信頼区間と自由度が決まったら、$t$分布表を用いて統計量$t$に対する信頼区間を求めます。
信頼区間90%、95%、99%、自由度1〜10のt分布表は以下となります。
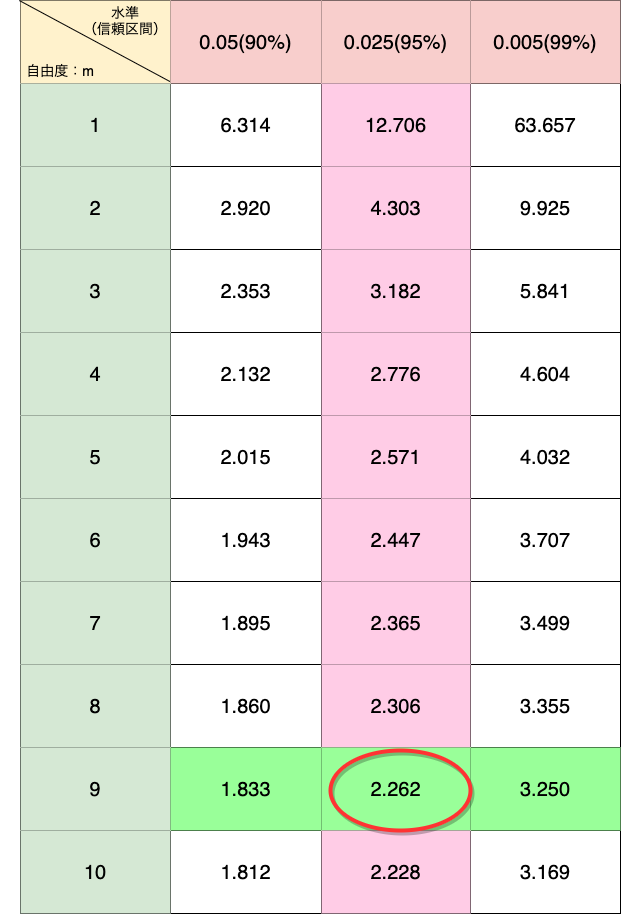
t分布表から、95%の信頼区間と自由度:9の値は2.262となります。
よって、統計量$t$に対する95%の信頼区間は以下のようになります。
$$ -2.262 \leq t \leq 2.262 $$
以上より、統計量$t$の信頼区間を形成することができました。
母平均を推定する区間推定(母分散がわからない場合)の手順 その4:統計量$t$から母平均$\mu$を推定
最後は、算出した統計量$t$と統計量$t$の信頼区間から、母平均$\mu$を推定します。
手順2、手順3で算出した統計量$t$と信頼区間から以下のようにあらわすことができます。
$$ -2.262 \leq t \leq 2.262 $$
$$ -2.262 \leq \frac{176.54-\mu}{\sqrt{\frac{47.86}{10}}} \leq 2.262 $$
$$ -2.262 \times \sqrt{\frac{47.86}{10}} \leq 176.54 – \mu \leq 2.262 \times \sqrt{\frac{47.86}{10}} $$
$$ 176.54-2.262 \times \sqrt{\frac{47.86}{10}} \leq \mu \leq 176.54 + 2.262 \times \sqrt{\frac{47.86}{10}} $$
$$ 171.59 \leq \mu \leq 181.49 $$
よって、成人男性の身長の平均値は、95%の信頼区間で171.59cm以上、181.49cm以下であると推定できました。
以上が、母分散がわからないときの区間推定の手順となります。
標本から母平均を推定する区間推定(母分散がわからない場合):まとめ
いかがでしたでしょうか?以下まとめです。
- 母分散がわからない場合、標本平均$\bar{X}$、標本の数$n$、不偏分散$\U^2$から母平均を推定できる
- 母平均を推定する場合、自由度とt分布を利用する
みなさんも、得られたデータから母平均の推定にチャレンジしてみていくださいね!
最後まで、この記事を読んでいただきありがとうございました!





コメント