こんにちは、かじつとむです。
今までさまざまな確率について解説してきました。
今回は、確率から実数値を計算する期待値について解説します。
この期待値を理解することで、確率からどのくらいのデータになるのか理解できます。
この記事を読むことで以下のことがわかります。
- 期待値について理解できる
- 期待値の計算方法やビジネスへの活用方法について理解できる
それではいってみましょう!
【統計学で使う確率を理解する】期待値とは
期待値とは、1回の試行で得られる値の平均値です。
たとえば、宝くじを買ったときにどのくらい金額がもどってくる値などをいいます。
一般的には確率変数に確率をかけあわせて、それらをすべて足し合わせることで得られる値となります。この値は、確率分布の観点から見るとデータの平均値とも呼ばれます。
では具体的に期待値を計算してみましょう!
たとえば、コイン2枚を投げた時の表が出る枚数の期待値を考えます。
まず、コインを2枚投げたときの起こりうるすべての現象を考えます。
コインを2枚投げたときの表が出る枚数はそれぞれ0枚、1枚、2枚となります。
次にそれぞれの起こりうる現象に対する確率を計算します。
今回の場合は表が0枚のとき、1枚のとき、2枚のときの確率を計算します。
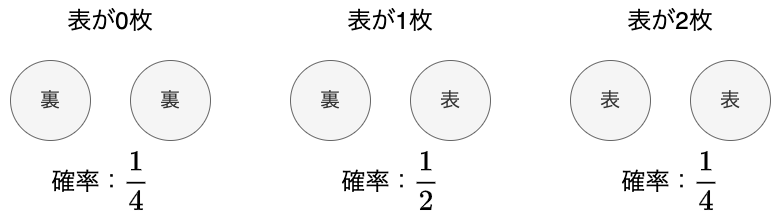
表が0枚の確率は1/4、表が1枚の確率は1/2、表が2枚の確率は1/4となりますので、期待値は以下のように計算すると算出できます。
$$ \begin{eqnarray}
表の期待値 = 0枚 \times \frac{1}{4} + 1枚 \times \frac{1}{2} + 2枚 \times \frac{1}{4} \\
= \frac{1}{2}枚 + \frac{1}{2}枚 \\
= 1枚
\end{eqnarray} $$
よって、コイン2枚を投げたときの表が出る枚数の期待値は1枚になります。
以上が期待値の概要になります。次は一般的な期待値の計算方法について詳しく解説します。
【統計学で使う確率を理解する】期待値の計算方法
期待値の計算方法は、確率分布が離散分布か連続分布かによって異なります。
期待値の計算方法 その1:離散分布の期待値
離散分布の場合、確率変数が$x_{i}$のときの確率を$f_{i}$としたとき、その期待値は以下のように計算できます。
$$ 期待値:E(x) = \sum_{i = 1}^{\infty} x_{i}f_{i}$$
まず期待値についてはExpected valueと呼ばれることから、確率変数$x$を用いて$E(x)$と表記されます。
次に$\sum_{i = 1}^{\infty}$は変数$i$を1〜$\infty$まで足し合わせる記号です。
よって、$\sum_{i = 1}^{\infty} x_{i}f_{i}$は確率変数$x_{i}$とその確率$f_{i}$をかけ合わせて、それらをすべて足し合わせるという意味になります。
実は先ほどの例で紹介したコイン2枚を投げたときの表が出る枚数の期待値の計算方法と同じになります。
この場合、確率変数をコインの表の枚数とします。
0枚に対する確率が1/4、1枚に対する確率が1/2、2枚に対する確率が1/4となりますので、それぞれをかけ合わせて足し合わせることで期待値を計算しているのです。
また、確率変数$x$に対して得られる結果を$g(x)$とすると、$g(x)$に対する期待値$E(g(x))$は以下のように計算できます。
$$ 期待値:E(g(x)) = \sum_{i = 1}^{\infty} g(x_{i})f_{i}$$
これは確率変数$x$によって得られる結果の期待値も計算することができるという意味です。
たとえば、コインを2枚投げたときの表の枚数に対して点数をつけるとその点数の期待値を計算することができます。
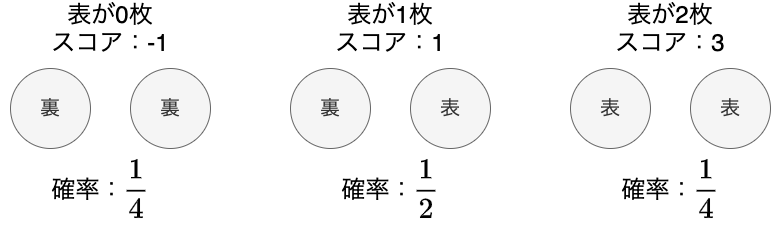
表の枚数が0枚のとき点数をー1、1枚のとき点数を1、2枚のとき点数を3とすると、点数の期待値は以下のように計算できます。
$$ \begin{eqnarray}
スコアの期待値 = -1 \times \frac{1}{4} + 1 \times \frac{1}{2} + 3 \times \frac{1}{4} \\
= -\frac{1}{4} + \frac{1}{2} + \frac{3}{4} \\
= 1
\end{eqnarray} $$
よって、点数の期待値は1となります。
以上のように、確率変数に対して得られる結果の期待値も計算できます。
期待値の計算方法 その2:連続分布の期待値
連続分布の場合、確率変数$x$となる確率が$f(x)$の関数(確率密度関数)に従うとき、その期待値は以下のように計算できます。
$$ 期待値:E(x) = \int_{-\infty}^{\infty} xf(x) dx $$
離散分布と比較すると、$xf(x)$が確率変数$x$と確率密度関数$f(x)$をかけ合わせているという意味になります。
そして、これらを足し合わせるという意味で$-\infty$から$\infty$までの積分を行うことで連続分布に対する期待値の計算を可能にしています。
たとえば、確率変数$x$に対する確率密度関数$f(x)$を以下のように定義したときの期待値を計算する場合を考えてみましょう。
$$ \begin{eqnarray}
f(x)
=
\begin{cases}
\frac{1}{2} & ( 0 \leq x \leq 10 ) \\
0 & ( x \lt 0, x \gt 10 )
\end{cases}
\end{eqnarray} $$
この場合以下のように期待値を計算します。
$$ \begin{eqnarray}
期待値:E(x) &=& \int_{-\infty}^{\infty} xf(x) dx \\
&=& \int_{-\infty}^{0} xf(x) dx + \int_{0}^{10} xf(x) dx + \int_{10}^{\infty} xf(x) dx \\
&=& \int_{-\infty}^{0} x \times 0 dx + \int_{0}^{10} x \times \frac{1}{2} dx + \int_{10}^{\infty} x \times 0 dx \\
&=& \int_{0}^{10} \frac{1}{2} x dx \\
&=& \left[ \frac{1}{4} x^2 \right]_0^{10} \\
&=& \frac{100}{4} – 0 \\
&=& 25
\end{eqnarray} $$
以上のように連続分布に対する期待値を計算します。
また、確率変数$x$に対して得られる結果を$g(x)$とすると、$g(x)$に対する期待値$E(g(x))$は以下のように計算できます。
$$ 期待値:E(g(x)) = \int_{-\infty}^{\infty} g(x)f(x) dx$$
以上のように、連続分布であっても確率変数に対して得られる結果の期待値も計算できます。
期待値の計算方法がわかったところで次は期待値をビジネスでどのように使うかについて解説します。
【統計学で使う確率を理解する】ビジネスで使う期待値
期待値をビジネスで使うことで、より具体的な数値での判断を可能にします。
たとえば、以下のプロジェクトに関して実行すべきかやめるべきかについて考えてみます。
プロジェクトAは成功すれば600万円の利益が発生し、失敗したら300万円の損失が発生すると考えられる。この場合、プロジェクトの成功率を仮に50%とした場合、このプロジェクトを行うべきか?
このようなときに利益がどのくらい発生するかの期待値を考えることで、プロジェクトを行うべきかどうかの判断ができます。利益の期待値は以下のように計算します。
$$ \begin{eqnarray}
利益の期待値 = 600万円 \times \frac{1}{2} – 300万円 \times \frac{1}{2} \\
= 300万円 – 150万円 \\
= 150万円
\end{eqnarray} $$
よって利益の期待値は150万円となりますので、プロジェクトAは実行すべきと判断できます。
このようにビジネスシーンで何かを判断するときに、どのくらいの確率で成功するのか、成功したときの報酬はどのくらいなのか、失敗のリスクはどのくらいかを期待値で見ることにより、より良い判断を可能にします。
【統計学で使う確率を理解する】期待値について:まとめ
いかがでしたでしょうか?以下まとめです。
- 期待値とは、1回の試行で得られる平均値
- 期待値は、確率変数に確率をかけ合わせて、それらを足し合わせることで得られる値
- 期待値は、確率が離散分布か連続分布かで計算方法が異なる
- 期待値をビジネスシーンで活用することでより具体的な数値での判断を可能にする
みなさんもぜひ期待値の勉強をして、ビジネスで活用できるようになりましょう!
確率などの統計学をもっと勉強したい方へ
期待値などの確率を使ったより高度な統計学についてもっと勉強したい方は「入門 統計解析法」という本がおすすめです。
この本では、基本統計量・ヒストグラム・確率分布・正規分布といった基礎的な内容から、実務で使う推定・検定・分散分析・回帰分析までを網羅的に学ぶことができます。
また、実務で使う統計学については、特に製造現場の実例を用いながら勉強することができますので、具体的なイメージを持って統計学を勉強することができる一冊となります。
高校数学までの勉強は必要となりますが、それさえ勉強できていれば、統計学全体を理解するのにおすすめの本となります。
統計学の基礎を勉強してみたい、実務での統計学の例を見ながら統計学を学びたい方にとってはぜひ手に取ってみてほしい本となります。
みなさんもぜひ統計学について学んでみてくださいね!
最後までこの記事を読んでいただきありがとうございました!
統計学を動画で勉強したい方へのおすすめの動画講座はこちら
![]()




コメント