こんにちは、かじつとむです。
みなさんはベイズ統計学という言葉を聞いたことがあるでしょうか?
ベイズ統計学はAIや機械学習、ビッグデータ等に使用されている重要な統計学の1つです。
しかし、ベイズ統計学は普通の統計学とは違いかなり特殊です。
今回はそんなベイズ統計学について入門者向けにできるだけ簡単に解説します。
この記事を読むと以下のことがわかります。
- ベイズ統計学の基礎について理解できる
- ベイズ統計学の具体的な使い方について理解できる
それではいってみましょう。
【入門者向け】ベイズ統計学とは
ベイズ統計学とは事前確率を設定し、情報を入れることで事後確率を予測する推定方法のことをいいます。
事前確率とは、データを手に入れる前に想定した確率のことをいいます。
この事前確率は主観的、すなわち自分で好き勝手に決めても良い確率です。
たとえば、目の前の人の体調が悪いという確率は人によってさまざまに感じると思います。5%の確率で体調が悪いと考えるかもしれませんし、30%の確率で体調が悪いと感じるかもしれません。
このように人によって変わっていく確率を主観的な確率といい、ベイズ統計学はこの主観的な確率を設定するところからスタートとなります。
事後確率とは、データを用いて事前確率を修正した確率のことをいいます。
先ほどの例で、目の前の人の体調が悪いという事前確率を30%とします。次に目の前の人がマスクをしていたことがわかり、この情報を受けて目の前の人が体調が悪い確率を60%と修正します。
このように、マスクをしたという情報を受けて修正した確率を事後確率といいます。
また情報を受けて事後確率を更新したことをベイズ更新ともいいます。
ベイズ統計学の概要がなんとなくわかったところで、次はベイズ統計学の具体的な使い方について解説します。
【入門者向け】ベイズ統計学の使い方
では具体的にベイズ統計学の使い方について具体例を用いて説明します。
本来はベイズの定理がありますが、今回は直感的かつ四則演算のみで使う方法を教えます。
ベイズ統計学のプロセスは以下の通りになります。
- タイプ別の事前確率の設定
- 各タイプの行動についての条件つき確率の計算
- 行動の指定
- 事後確率の計算
また、今回は商品を購入するかどうかを例として説明します。
【入門者向け】ベイズ統計学の使い方1:タイプ別の事前確率の設定
まず、タイプ別の事前確率を設定します。
今回の場合、商品を購入する人としない人の2タイプにわけることができます。
事前確率は主観的な確率を用いますので、設定する確率はなんでも良いです。
今回の場合、商品を購入する人の確率を20%(0.20)とし、購入しない人の確率を80%(0.80)と設定します。
この確率を図で表すと以下のようになります。

これは購入する人としない人の2つの世界があるというイメージを持っていただくだけで結構です。
【入門者向け】ベイズ統計学の使い方2:各タイプの行動についての条件つき確率の計算
次に、各タイプごとの行動についての条件つき確率を計算します。
この計算には何かしらのデータや経験則が必要になってきます。
今回の例では、商品を購入した人としない人で広告を見たかどうかを調べたとします。すると、商品を購入した人が広告を見た確率が80%(0.80)、商品を購入しなかった人が広告を見た確率が50%とわかりました。
これらの情報を表でまとめると以下のようになります。

表では、商品を購入した人が広告を見た確率は80%(0.80)であるため、商品を購入した人が広告を見ていない確率は20%(0.20)となります。同様に商品を購入していな人が広告を見た確率は50%(0.50)であるため、商品を購入していない人が広告を見ていない確率は50%(0.50)となります。
ここで重要なのは広告を見た人が商品を購入した確率はまだ計算されていないことです。
なぜなら、これは商品を購入した人の広告を見た人の確率であって、実際に広告を見た人の商品を購入した確率を計算しているわけではないからです。
では、どのようにすれば広告を見た人が商品を購入した確率を計算すれば良いのでしょうか?
答えは全体から商品を購入した確率と商品を購入した人が広告を見た確率をかけることで計算できます。少しわかりづらいと思いますので以下の図で表します。

上の図は、先ほど設定した商品を購入するかしないかの事前確率と広告の情報をまとめたものです。
すると商品を購入する×広告を見る、商品を購入しない×広告を見る、商品を購入する×広告を見ない、商品を購入しない×広告を見ないという4つの世界にわけることができます。
このようにそれぞれの世界同士の割合をかけ合わせることで、それぞれの条件つきの確率を計算することができます。
広告を見た人が商品を購入する確率を計算する場合、0.2 × 0.8 = 0.16となります。
また、すべての起こっている確率を足し合わせると1になることも覚えておきましょう。具体例では0.16 + 0.04 + 0.40 + 0.40 = 1となっています。
ここまでが事後確率を計算する準備です。
【入門者向け】ベイズ統計学の使い方3:行動の指定
先ほどはすべての起こっている確率について計算しました。
今度は行動を限定して確率の計算を行います。そのために、行動を指定します。
なぜ、行動を指定する必要があるのでしょうか?
答えは行動によってその後の確率が変化してしまうからです。
たとえば、5本のくじのなかにあたりが2本あったとします。自分は2番目にくじを引くことになったとしましょう。
この場合、あたりを引く全体の確率は2/5となります
では、最初に引いた人のくじがあたりだとわかっている場合どうでしょうか?
答えは4本のくじの中にあたりが1本だけになりますので、確率は1/4と小さくなってしまいます。
このように行動を指定することで確率が変化します。
では先ほどの商品の購入に対して、広告を見たという行動を指定して確率を考えていきましょう。
広告を見たという行動に着目した場合の確率について以下の図で表します。
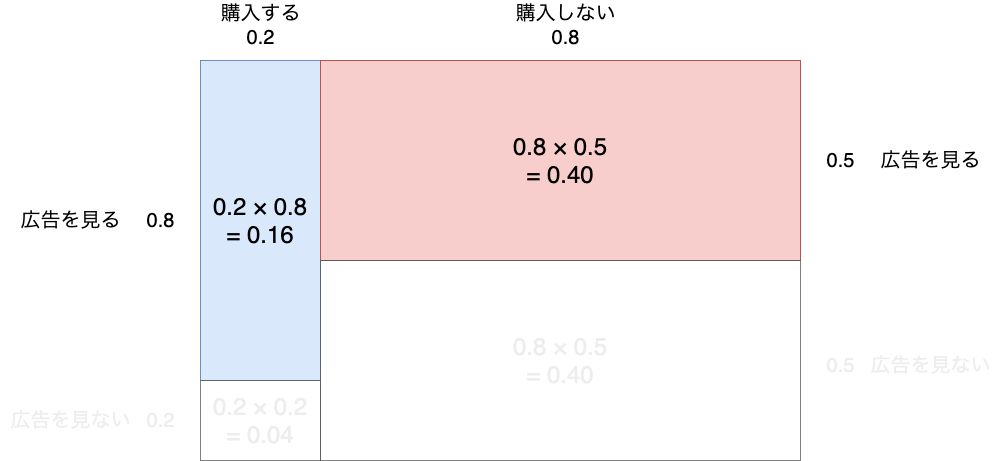
広告を見たという行動に着目するということは、それ以外の行動の確率を消してしまえば良いということになります。
今回の場合は広告を見ないという行動を消して確率を考えれば良いということになります。簡単ですね!
しかし、ここで1つ問題が発生します。広告を見ないという行動を消して確率を考える場合、すべての確率を足し合わせても1にならないということです。広告を見るという行動だけを指定した結果、0.16 + 0.40 = 0.56となり、確率の定義と反してしまします。
このため、行動を指定した後に確率を計算しなおす必要があります。
ベイズ統計学の使い方4:事後確率の計算
最後にもう一度確率を計算しなおします。ではどのように確率を計算しなおせば良いのでしょうか?
答えは、先ほど足し合わせた確率でそれぞれの確率を割れば良いことになります。
少し難しいと思いますので、実際にやって見ながら説明します。まず先ほどの広告をみるという行動の確率の足し合わせを式で表してみましょう。
$$ 0.16 + 0.40 = 0.56 $$
次にこの式すべてを、先ほど足し合わせた確率0.56で割ってみましょう。
$$ \frac{0.16}{0.56} + \frac{0.40}{0.56} = \frac{0.56}{0.56} $$
このような等式が成り立ちます。あとはそれぞれ約分します。
$$ \frac{2}{7} + \frac{5}{7} = 1 $$
するとそれぞれの確率を導きだすことができ、かつ足し合わせた確率が1となりました。
このようにすべて足し合わせた確率を1と見なすために、足し合わせた確率で割ることでそれぞれ商品を購入する確率、購入しない確率を計算できるということができます。
最後に広告を見た場合の考察をしましょう。広告を見て商品を購入する確率は0.16 / 0.56 = 2 / 7 = 0.285….すなわち、おおよそ28.5%になります。
ちなみに事前確率として設定した商品を購入する確率は20%でした。
この2つを比較すると広告を見た場合、商品を購入する確率が上がったということです。すなわち、広告を出すことは商品を購入するのに効果があったことがわかります。
このように事前確率を設定し、情報を入れることで事後確率を計算していくのがベイズ統計学です。
【入門者向け】ベイズ統計学を理解とは:まとめ
いかがでしたでしょうか?以下まとめです。
- ベイズ統計学とは事前確率を設定し、情報を入れることで事後確率を予測する推定方法
- ベイズ統計学はタイプ別の事前確率を設定し、データから各タイプの条件確率を計算する。その後に行動を指定して、事後確率を計算する
今回は少し難しかったかもしれませんが、ベイズ統計学は仮説を検証したり、効果の確認をするのにとても有効な手段ともいえます。ぜひベイズ統計学を使ったデータ分析にチャレンジしてみましょう!
この記事を最後まで読んでいただきありがとうございました!
ベイズ統計学を勉強したい方へ
ベイズ統計学についてもっとよく勉強したい方は「完全独習 ベイズ統計学入門」がおすすめです。
この本では、ベイズ統計学についてできる限りわかりやすく解説しています。
この本の著者、小島 寛之さんは「完全独習 統計学入門」といった統計学をできる限りわかりやすく、かつ難しい数式を使わないで解説している本を書いている方です。
今回の「完全独習 ベイズ統計学入門」についてもできる限り難しい数学を使わないで、かつ、面積図といった本来のベイズ統計学とは、異なった視点で解説しているので、入門者だけではなく、ベイズ統計学を教える人も必見の内容となっております。
ベイズ統計学を初めて勉強する方やベイズ統計学をどうやって教えれば良いかわからない方には、ぜひ手に取ってもらいたい一冊となります。
みなさんもぜひベイズ統計学について勉強してみましょう!
最後までこの記事を読んでいただきありがとうございました!
ベイズ統計学の基礎からプログラミングの実装までを動画で学びたい方はこちら!
![]()




コメント