こんにちは、かじつとむです。
2回にわたって標本から母集団を推定する方法について解説してきました。
3回目の今回は、区間推定について説明します。
この記事を読むことで以下のことがわかります。
- 区間推定とはどういうものなのか理解することができる
- 母分散がわかっている場合の区間推定の方法を理解することができる
それではいってみましょう!
標本から母平均を推定する区間推定:区間推定とは
区間推定とは、母集団の分布が正規分布であると仮定したときに、標本から得られた統計量を使って、ある程度の区間を持って母平均などを推定する方法です。
母平均などを推定する区間を信頼区間といいます。
母平均の区間推定は、母分散がわかっている場合とそうでない場合によって推定方法が異なります。
母分散がわかっている場合、標本平均$ \bar{X} $、標本の数$ n $、そして、母分散$ \sigma^2 $と標準正規分布を使って信頼区間を算出します。
母分散がわかっていない場合、標本平均$ \bar{X} $、標本の数$ n $、そして、標本から得られる不偏分散$ U^2 $とt分布を使って信頼区間を算出します。
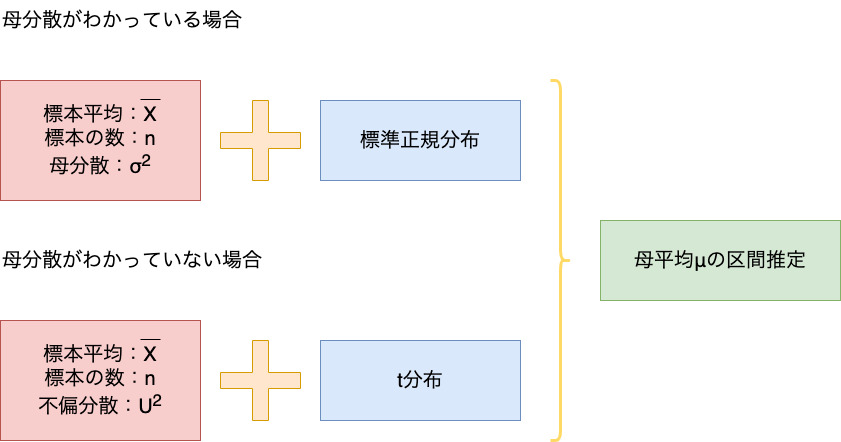
今回は、母分散がわかっている場合の区間推定について解説します。
母平均を推定する区間推定(母分散がわかる場合):標準正規分布とは
母分散がわかる場合の区間推定を理解するにあたって、標準正規分布について理解する必要があります。
標準正規分布とは、平均値が0で標準偏差が1の正規分布です。以下に標準正規分布の図を示します。
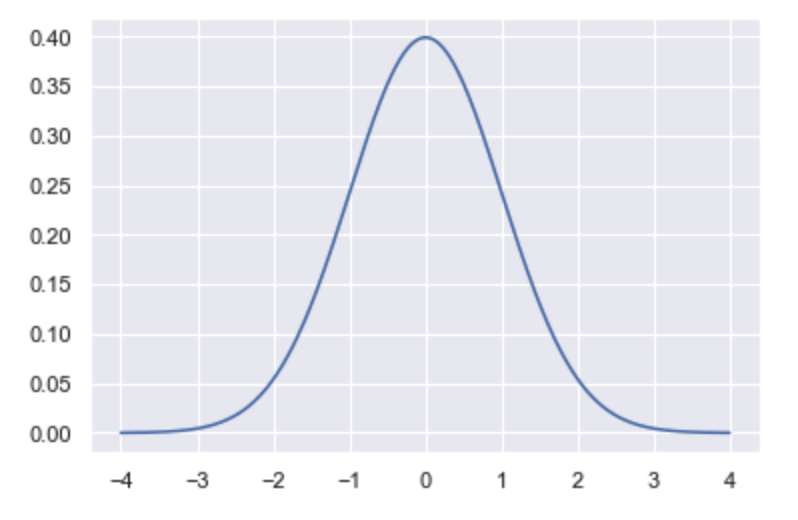
標準正規分布の縦軸は確率密度といい、この値が大きければ大きいほど横軸の値である可能性が高いという意味です。
標準正規分布は、とりうる値のなかで0が最も可能性がたかく、±1、±2、±3ととりうる値が大きくなれば大きくなるほど、その可能性が小さくなっていきます。
これを利用すると、とりうる値が±1の範囲にデータがある可能性は68.26%、±2の範囲では95.44%というように、任意の確率でデータが存在するかどうかを判断することができます。
すなわち、標準正規分布を使えば、ある値が任意の確率でどのくらいの範囲に存在しているかを算出することができます。
ではどうすれば標準正規分布にすることができるのでしょうか?
答えは標準化をすることです。標準化は次で解説します。
母平均を推定する区間推定(母分散がわかる場合):標準化とは
標準化とは、得られたデータの平均値を0、分散(標準偏差)を1にするデータの変換方法です。
これは、あたえられたデータを標準正規分布としてあつかえるように変換することを意味しています。
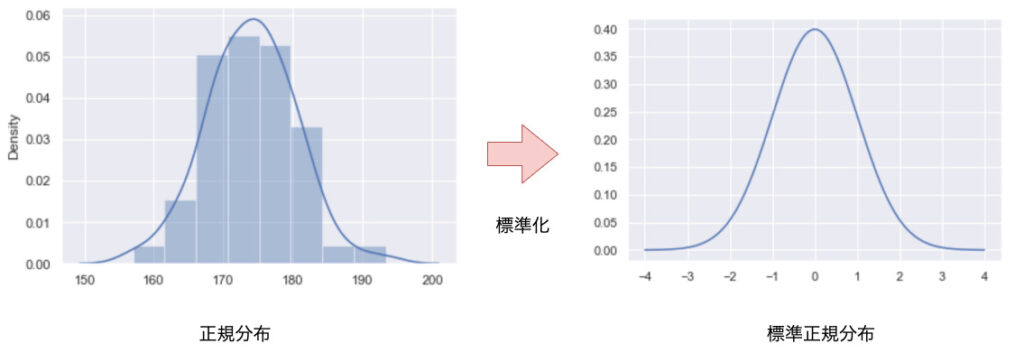
標準化をするときの統計量を$ Z $とあらわします。
まず、標本1つ$ x $に対して標準化をしますと、母平均$ \mu $、母分散$ \sigma^2 $を使って以下のようにようにあらわすことができます。
$$ Z = \frac{x – \mu}{\sigma} $$
まず、標本に対して母平均を引くことで、平均値0に対してのばらつきだけの値にします。
このばらつきを母分散の平方根、すなわち標準偏差で割ることで分散を1にすることで標準化が完了となります。
では、標本平均に対して標準化するとどうなるのでしょうか?
これは、母平均$ \mu $、母分散$ \sigma^2 $とさらに標本の数$ n $を使って以下のようにあらわします。
$$ Z = \frac{\bar{X} – \mu}{\frac{\sigma}{\sqrt{n}}} $$
標本1つと同様、標本平均に対して母平均を引き、平均値0に対するばらつきだけの値にします。
次に、母分散を標本の数で割った値の平方根で、先ほどのばらつきを割ることで標準化をします。
なぜ、母分散を標本の数で割った値の平方根で割る必要があるのでしょうか?
これは中心極限定理によるものです。
中心極限定理とは、母集団から標本を抽出するとき、標本平均の分布が大きくなるにつれて、平均が母平均の$ \mu $、分散が$ \frac{\sigma^2}{n} $の正規分布に近づくというものです。
もう少し噛み砕いていうと、標本の数が大きいほど分散は小さくなり、その分散が$ \frac{\sigma^2}{n} $になるということです。
標準化で分散(標準偏差)を1にするには、正規分布の分散の平方根で割る必要があります。
ですので、分散$ \frac{\sigma^2}{n} $の平方根$ \frac{\sigma}{\sqrt{n}} $で割る必要があったというわけです。
ここまでが母分散がわかっている場合の区間推定の準備となります。
次は、区間推定の手順について具体例を用いて解説します。
母平均を推定する区間推定(母分散がわかる場合):区間推定の手順
母分散がわかっている場合の区間推定の手順を以下にまとめます。
- 推定したい標本に対して、標本平均を算出する
- 標本平均、母分散、標本の数と母平均$\mu$を用いて、統計量Zを算出する
- 求めたい信頼区間(何パーセントの精度)から統計量Zの信頼区間を形成する
- 統計量Zの信頼区間を母平均$\mu$であらわす
この手順を、以下の例に当てはめながら計算していきましょう!
成人男性10人の身長のデータから、成人男性全体の身長の母平均を区間推定したい。
ただし、母分散は$6^2$とし、信頼区間は95%とする。また、成人男性10人の身長のデータは以下にあらわす。
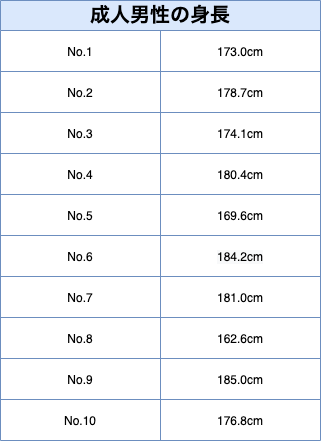
母平均を推定する区間推定(母分散がわかる場合)の手順 その1:標本平均の算出
まずは、得られたデータから標本平均を算出します。
標本平均は以下のように算出することができます。
$$ 標本平均: \bar{X} = \frac{データの合計}{データの数} = \frac{173.0 + 178.7 + \cdots + 176.8}{10} = 176.54 $$
よって、標本平均:176.54cmを算出することができました。
母平均を推定する区間推定(母分散がわかる場合)の手順 その2:統計量Zの算出
次に、統計量Zを算出します。
統計量Zは、先ほど算出した標本平均:176.54と、母分散:$6^2$、標本の数:10、
母平均:$\mu$を用いて以下であらわすことができます。
$$ 統計量:Z = \frac{\bar{X} – \mu}{\frac{\sigma}{\sqrt{n}}} = \frac{176.54 – \mu}{\frac{6}{\sqrt{10}}}$$
以上のように、統計量Zを母平均$\mu$を用いてあらわすことができました。
母平均を推定する区間推定(母分散がわかる場合)の手順 その3:統計量Zの信頼区間の形成
次に、統計量Zの信頼区間を形成します。
この手順は、まず求めたい信頼区間を決めます。
たとえば、ざっくりとした推定の場合は信頼区間90%、確実に推定したい場合は99%といった感じです。
一般的に区間推定を行う場合の信頼区間は95%といわれています。また今回の例も信頼区間は95%としているので、これを用いましょう。
求めたい信頼区間を決めたら、統計量Zの信頼区間を求めます。
この信頼区間を決めるには、本来であれば標準正規分布表を用いますが、今回は代表的な信頼区間90%、95%、99%のときの統計量Zの信頼区間を以下にまとめます。
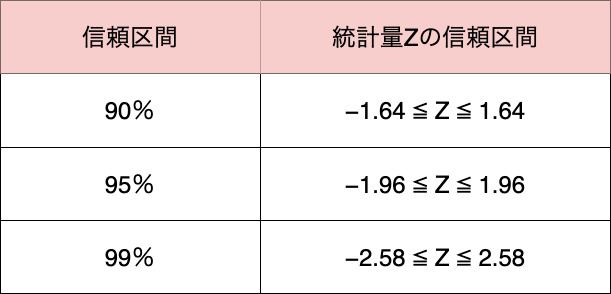
このように信頼区間から統計量Zの信頼区間を求めることができます。
また、信頼区間が大きいほど、統計量Zの信頼区間の幅も大きいことがわかります。
今回は信頼区間95%で区間推定をするため、-1.96以上、1.96以下のときの統計量Zを算出すればよいということになります。
母平均を推定する区間推定(母分散がわかる場合)の手順 その4:統計量Zの信頼区間から母平均$\mu$を推定
最後に、算出した統計量Zと統計量Zの信頼区間から母平均$\mu$を推定します。
手順2、手順3で算出した統計量Zと信頼区間から以下のようにあらわすことができます。
$$ -1.96 \leq Z \leq 1.96 $$
$$ -1.96 \leq \frac{176.54 – \mu}{\frac{6}{\sqrt{10}}} \leq 1.96 $$
$$ -1.96 \times \frac{6}{\sqrt{10}} \leq 176.54 – \mu \leq 1.96 \times \frac{6}{\sqrt{10}} $$
$$ 176.54 -1.96 \times \frac{6}{\sqrt{10}} \leq \mu \leq 176.54 + 1.96 \times \frac{6}{\sqrt{10}} $$
$$ 172.28 \leq \mu \leq 179.72 $$
よって、成人男性の身長の平均値は、95%の信頼区間で172.28cm以上、179.72cm以下であると推定できました。
以上が、母分散がわかるときの区間推定の手順となります。
標本から母平均を推定する区間推定:まとめ
いかがでしたでしょうか?以下まとめです。
- 区間推定とは、母集団の分布が正規分布であると仮定したときに、標本から得られた統計量を使って、ある程度の区間を持って母平均を推定する方法
- 母分散がわかっている場合、標本平均$ \bar{X} $、標本の数$ n $、そして、母分散$ \sigma^2 $と標準正規分布を使って区間推定を行う
- 母分散がわかっている場合の区間推定は、標準正規分布と標準化を使って推定することができる
みなさんも、区間推定にチャレンジしてみてください!
最後まで、この記事を読んでいただきありがとうございました!





コメント