こんにちは、かじつとむです。
みなさんは共分散ってご存知でしょうか?
共分散を理解することで、2つのデータの関係性を理解するのに重要な統計量です。
そして、回帰分析といった高度な統計学を理解するのに必要な統計量でもあります。
今回はそんな共分散について解説します。
この記事を読むことで以下のことがわかります。
- 共分散の基本的な内容について理解できる
- 共分散の計算方法について理解できる
- 共分散をExcelで求める方法について理解できる
それではいってみましょう!
共分散とは
共分散とは、2つの変数の関係をあらわす統計量です。
たとえば、$x$と$y$の2変数に対する共分散を考えてみましょう。
共分散が正の値で、大きな値である場合「$x$が大きいと、$y$も大きくなる傾向になる」といった関係を示します。このように一方の値が増加すると、もう一方の値が増加する関係を正の相関といいます。
共分散が負の値で、大きな値である場合「$x$が大きいと、$y$は小さくなる」といった関係を示します。このように一方の値が増加すると、もう一方の値が減少する関係を負の相関といいます。
また、共分散が0に近い場合、「$x$が大きくても小さくても$y$はほとんど変わらない」といった関係を示します。このような関係を無相関といいます。
このように共分散を求めることで、2つの変数の関係性をあらわすことができます。
ただし、共分散では相関の強さについてはわかりません。
共分散では、単位による大きさの補正がかかっていないため、どのくらい大きければ強い相関なのか、弱い相関なのか示すことができません。
相関の強さがわかるには相関係数を求める必要があります。ただし、相関係数の計算に共分散が使われるため、共分散の意味を知っておくことは重要です。
共分散の基本的な内容について理解したところで、次は共分散の計算方法について解説します。
共分散の計算方法(定義式からの計算方法)
共分散は、それぞれ2変数のデータと平均値の差をかけ合わせた値の平均値を計算することで求めることができます。
具体的には、2つの変数を$x$, $y$としたとき、それぞれの平均値を$\bar{x}$,$\bar{y}$、データの値を$x_{i}$,$y_{i}$、データの個数を$n$としたとき、共分散$s_{xy}$は以下の計算式であらわすことができます。
$$ 共分散:s_{xy} = \frac{1}{n} \sum_{i=1}^{n} (x_{i} – \bar{x})(y_{i} – \bar{y}) $$
数式だと少しわかりづらいと思いますので、具体的な計算手順をまとめると以下のようになります。
- それぞれの変数の平均値を計算する
- それぞれの変数データと平均値の差(偏差)を計算する
- それぞれの変数の偏差をかけ合わせる
- 3で求めた値の平均値を計算する
それでは具体的な事例を使って共分散を計算してみましょう!
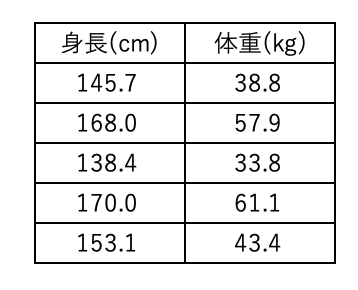
ある5人の身長と体重のデータがある。このときの身長と体重の共分散を計算せよ。
身長と体重のデータは以下である。
まずは共分散がどのような値か予測するために、2変数のデータを散布図であらわします。
身長を横軸、体重を縦軸として散布図を作成すると以下のようになります。
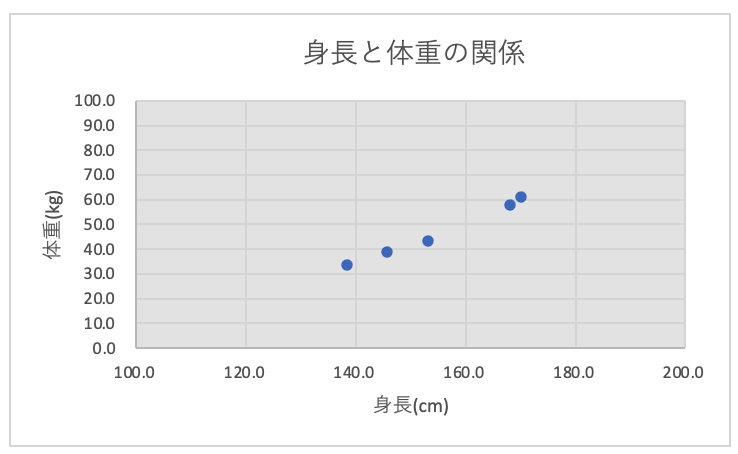
身長と体重の散布図を見るとおおむね右肩上がりの関係、すなわち身長が大きくなると、体重も大きくなることがわかります。
よって、共分散の値は正の値で大きな値を取ることが予測できます。
データの散布図を作成したら、次はいよいよ共分散の計算するためにまずは身長と体重の平均値を計算します。
平均値はデータの合計をデータの数で割ることで計算できます。
よって、身長および体重の平均値は以下のようになります。
$$ 身長の平均値: \bar{x} = \frac{145.7+168.0+138.4+170+153.1}{5} = 155.0 $$
$$ 体重の平均値: \bar{y} = \frac{38.8+57.9+33.8+61.1+43.4}{5} = 47.0 $$
身長と体重の平均値を計算したら、それぞれのデータに対する偏差を計算します。
偏差はデータと平均値の差で求めることができるので、以下のようになります。
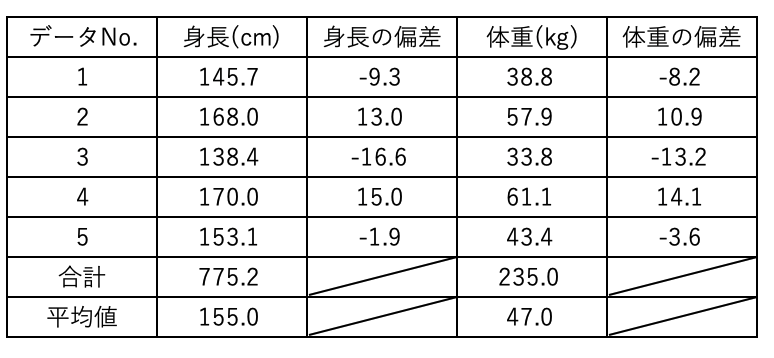
それぞれの変数に対する偏差を計算したら、次は2変数の偏差をかけ合わせ合計します。
それぞれの身長の偏差と体重の偏差をかけ合わせると以下のようにあらわすことができます。
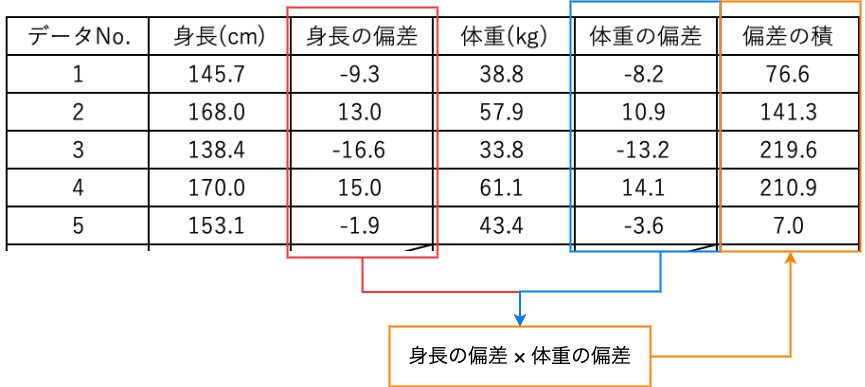
それぞれの身長の偏差と体重の偏差をかけ合わせた値を求めたら、最後にこの値の平均値を計算します。
平均値は合計してデータの数で計算できるので、以下のように求めます。
この値が身長と体重の共分散となります。
$$ s_{身長 \times 体重} = \frac{76.6+141.3+219.6+210.9+7.0}{5} = 131.08 $$
よって身長と体重の共分散は131.08となります。
共分散が正の値でかつ大きな値であることから、身長が大きいと体重も大きくなるといった正の相関があるということがいえます。
以上が共分散の計算方法です。ですがこの方法以外にも共分散の計算方法があります。
次は、共分散の公式について解説します。
共分散の計算方法(公式を使ったの計算方法)
共分散の公式は以下の通りです。
$$ 共分散:s_{xy} = \frac{1}{n} \sum_{i=1}^{n} x_{i} y_{i} – \bar{x} \bar{y} $$
すなわち、それぞれの2変数のかけ合わせた値の平均値からそれぞれの変数の平均値をかけたもので引くことで共分散を計算することができます。
一見、定義とは違うように見えますが、実は定義式からこの公式を求めることができます。
まずは定義式から公式を証明します。定義式を分解すると以下のようになります。
$$ \begin{eqnarray}
共分散:s_{xy} &=& \frac{1}{n} \sum_{i=1}^{n} (x_{i} – \bar{x})(y_{i} – \bar{y}) \\
&=& \frac{1}{n} \sum_{i=1}^{n} (x_{i} y_{i} – x_{i} \bar{y} – y_{i} \bar{x} + \bar{x} \bar{y}) \\
&=& \frac{1}{n} (\sum x_{i} y_{i} – \bar{y} \sum x_{i} -\bar{x} \sum y_{i} + \bar{x} \bar{y} \sum 1) \\
&=& \frac{1}{n} \sum x_{i} y_{i} – \bar{y} \frac{1}{n} \sum x_{i} -\bar{x} \frac{1}{n} \sum y_{i} + \bar{x} \bar{y} \frac{1}{n} \sum 1
\end{eqnarray} $$
ここで$\frac{1}{n} \sum_{i=1}^{n} x_{i}$, $\frac{1}{n} \sum_{i=1}^{n} y_{i}$はそれぞれ変数$x$と$y$の平均値$\bar{x}$, $\bar{y}$とあらわすことができます。
また、\sum_{i=1}^{n} 1 は1を$n$回足すという意味なので$n$となります。
よって先ほど分解した共分散の定義式は以下のようになります。
$$ \begin{eqnarray}
共分散:s_{xy} &=& \frac{1}{n} \sum_{i=1}^{n} x_{i} y_{i} -\bar{y} \bar{x} – \bar{x} \bar{y} + \bar{x} \bar{y} \frac{1}{n} \times n \\
&=& \frac{1}{n} \sum_{i=1}^{n} x_{i} y_{i} – \bar{x} \bar{y} – bar{x} \bar{y} + bar{x} \bar{y} \\
&=& \frac{1}{n} \sum_{i=1}^{n} x_{i} y_{i} – \bar{x} \bar{y}
\end{eqnarray}$$
以上のように定義式から公式を求めることができます。
では公式を用いて共分散を計算してみましょう!
計算するデータは先ほどの身長と体重のデータとします。
公式を使った共分散の計算手順は以下の通りです。
- 2変数の平均値を計算する
- それぞれの2変数のデータをかけ合わせる
- かけ合わせた値の平均値を計算する
- 3で計算した値から2変数の平均値をかけ合わせたもので引く
まずは身長と体重のそれぞれの平均値を計算します。これは定義式からの共分散を計算する方法と同じです。
次からが定義式と違うところで、それぞれの2変数のデータをかけ合わせます。
かけ合わせた値は以下のようになります。
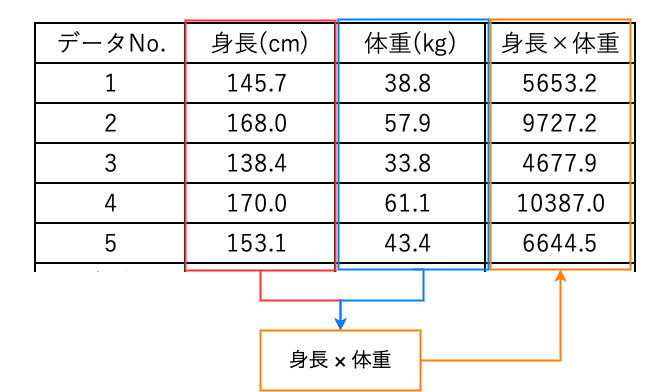
2変数のデータを掛け合わせたら、次はその平均値を計算します。
$$ \begin{eqnarray}
身長 \times 体重の平均値 &=& \frac{5653.2 + 9727.2 + 4677.9 + 10387.0 + 6644.5}{5} \\
&=& 7417.96
\end{eqnarray}$$
2変数のデータをかけ合わせた平均値を計算したら、その値から2変数の平均値をかけ合わせたもので引きます。
この値が身長と体重の共分散となります。
$$ s_{身長 \times 体重} = 7417.96 – 155.04 \times 47.00 = 131.08 $$
よって、身長と体重の共分散は131.08となり、定義式から計算した値と同じになりました。
このように2変数をかけ合わせた値の平均値からそれぞれの平均値をかけ合わせた値で引くことでも、共分散を計算することができます。
以上が共分散の計算方法になります。しかし非常に手間がかかると感じる人もいるかもしれません。
そこで最後にExcelを使った共分散の計算方法について解説します。
共分散の計算方法(Excelを使ったの計算方法)
共分散を計算するためのExcelの関数は以下の2通りです。
$$ = \mathrm{COVARIANCE.P(配列1, 配列2)} $$
$$ = \mathrm{COVAR(配列1, 配列2)} $$
たとえば、以下のExcelシートのように身長のデータをC27〜C31、体重のデータをD27〜D31にまとめたとします。
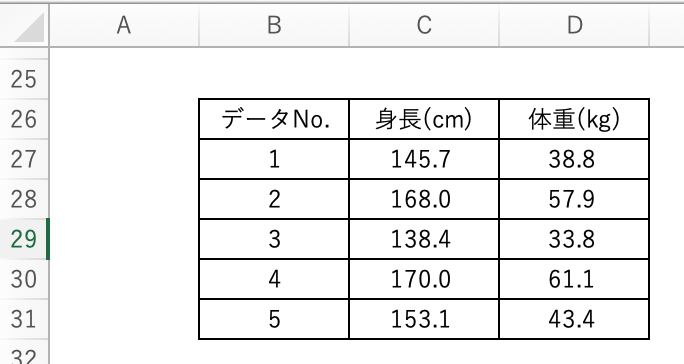
このとき、共分散の計算する場合、以下のように関数を適用します。
$$ = \mathrm{COVARIANCE.P(C27:C31, D27:D31)} $$
$$ = \mathrm{COVAR(C27:C31, D27:D31)} $$
以上のように関数を組み込むことで共分散を計算することができます。

共分散とは 基礎から計算方法 Excelでの求め方まで徹底解説:まとめ
いかがでしたでしょうか?以下まとめです。
- 共分散とは、2つの変数の関係をあらわす統計量
- 共分散の正負の値や大きさを見ることで、2つの変数の関係が正の相関であるか、負の相関であるかがわかる
- 共分散は、2変数のデータと平均値の差をかけ合わせた値の平均値を算出することで求めることができる
- 一方で、2変数のデータのかけ合わせた平均値から、それぞれの平均値をかけ合わせた値を引くことでも計算できる
- Excelでは$= \mathrm{CORVARIANCE.P(配列1, 配列2)}$や$= \mathrm{COVAR(配列1, 配列2)}$を使うことで簡単に計算することができる
みなさんもぜひ共分散を計算して、2つの変数の関係についてわかるようにしましょう!
より高度な統計学を勉強したい方へ
この記事を読んで、共分散を使った統計学(回帰分析や相関)について勉強したいと思った方は「入門 統計解析法」がおすすめです。
この本では、分散や標準偏差などの基本的内容から仮説検定・分散分析・回帰分析といった製造業の現場で実践的に使える統計学について学ぶことができます。
高校数学の内容までの数式を使いますが、実際の製造業で使われる具体例を用いて統計学を解説しておりますので、使い方をイメージできる一冊となります。
特に先ほど紹介した共分散についてや、共分散を相関・回帰分析に活用している例が記載されております。
数学の知識を持っており、実務で使える本格的な統計学を学びたい方にはぜひおすすめの本です!
みなさんもぜひ統計学の勉強にチャレンジし、ビジネスで活用できるようになったら幸いです。
最後までのこの記事を読んでいただきありがとうございました!
統計学を動画で勉強したい方はこちら!
![]()




コメント