こんにちは、かじつとむです。
前回の記事で共分散とはどういったものなのかについて解説しました。
共分散とは、2つの変数の関係をあらわす統計量です。
詳しい解説は以下の記事をご参照ください!
しかし共分散では、2つの関係性の強さまではあらわすことはできません。
この関係性をあらわすのに使われているのが相関係数となります。
今回は、そんな相関係数やそもそも相関とはどのようなものなのかについて解説します。
この記事を読むことで以下のことがわかります。
- 相関や相関係数がどういったものなのかについて理解できる
- 相関係数の計算方法について理解できる
それではいってみましょう!
相関とは
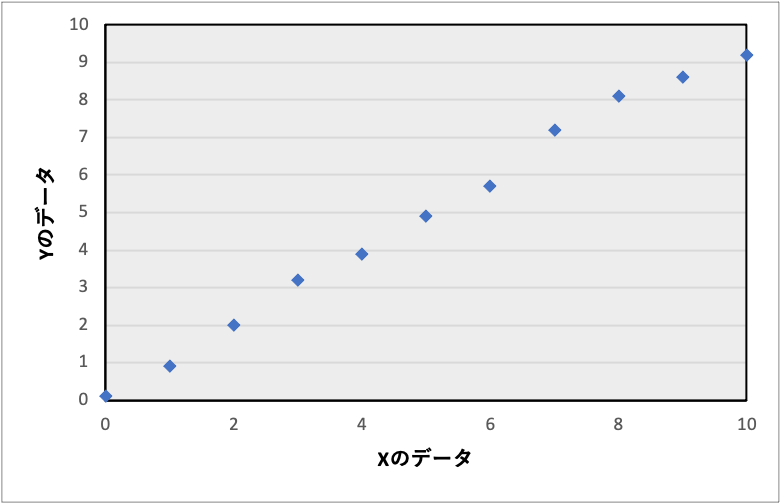
相関とは、2つのデータの直線的な関係のことをいいます。
たとえば、2つのデータに対してその関係性を散布図A, Bであらわしたとしましょう。
この場合、どちらが直線的な関係になるでしょうか?
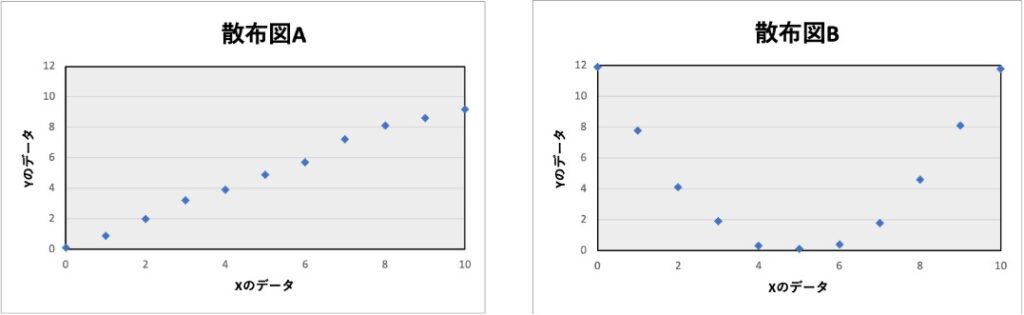
答えは、散布図Aの方が2つのデータが直線的な関係を示します。
このように、2つのデータを散布図であらわしその点が直線的に並んでいるかを確認することで、相関であるかを調べることができます。
ただし、相関を考える上で以下の2つの注意点があります。
- 相関ではなくても2つのデータには関係がある可能性がある
- 2つのデータが相関関係でも因果関係まではわからない
まずは、2つのデータは相関ではなくても何かしらの関係性がある可能性があります。
たとえば、先ほどの散布図Bでは相関の関係はありませんが、2次関数のような曲線の関係にはなっている可能性もあるからです。
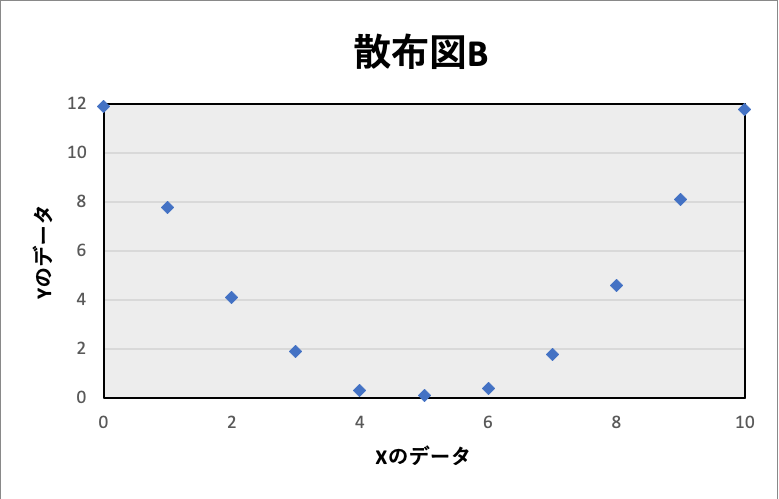
このように、必ずしも相関だけでデータの関係性を完全に把握することはできません。
よって、2つのデータの関係性を調べるには、まずは散布図でデータを見える化し、どのような関係性があるか目星をつけておくことが大切です。
もう1つの注意点は、2つのデータが相関関係であったとしても因果関係まではわからないということです。
これは有名な例として「アイスクリームの売り上げと水難事故の発生数」の話があります。
この話は「アイスクリームの売り上げと水難事故の発生件数の相関を調べたら、強い正の相関関係があることがわかった。よって、水難事故を減らすにはアイスクリームの販売を自粛すれば良いか?」という問題です。
しかし、実際これは間違いです。
理由は、アイスクリームの売り上げに対して水難事故の発生件数との因果関係が説明できないからです。
この問題の意図は、アイスクリームの売り上げと水難事故の発生件数にはどのような共通点があるかを考える必要があるということです。
たとえば、アイスクリームの売り上げと水難事故の発生件数は夏に多く発生しそうだ➡︎最高気温とアイスクリームの売り上げ、最高気温と水難事故の発生件数それぞれに因果関係がありそうだ、というように要因を深堀していく必要があります。
このように相関関係は必ずしも因果関係になることはないことを注意してください。
以上が相関についての概要となります。次は相関係数について解説します。
相関係数とは:概要と相関との関係
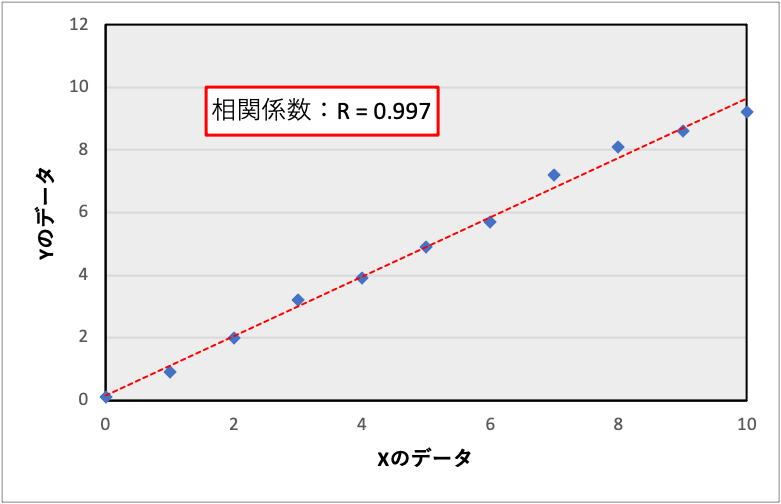
相関係数とは、相関の強さをあらわす指標で$r$とあらわされる値です。
相関係数は−1〜1までの値をとり、相関との関係は以下のようになります。

正の相関とは右肩上がりのグラフ、すなわち一方のデータが増大すれば、もう一方のデータも増大する関係のことをいいます。このとき相関係数は正の値をとり、1に近いほど強い正の相関となります。
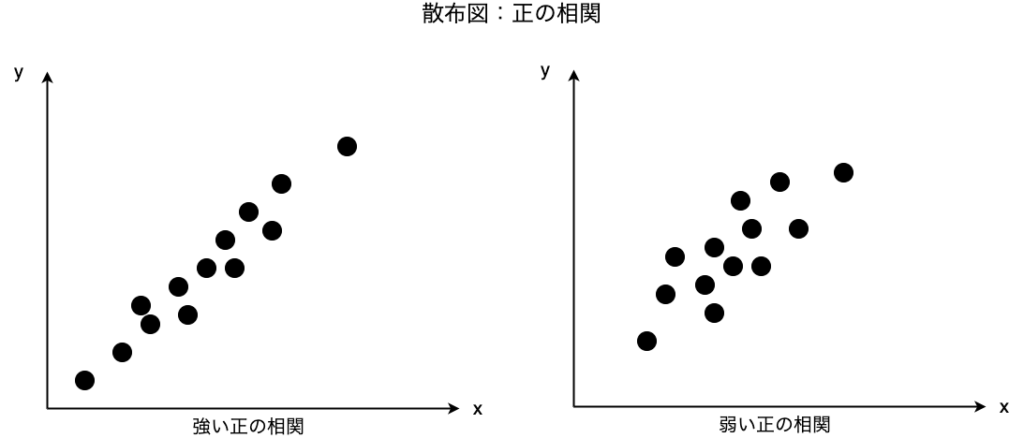
負の相関とは右肩下がりのグラフ、すなわち一方のデータが増大すると、もう一方のデータは減少する関係のことをいいます。このとき相関係数は負の値をとり、ー1に近いほど強い負の相関となります。
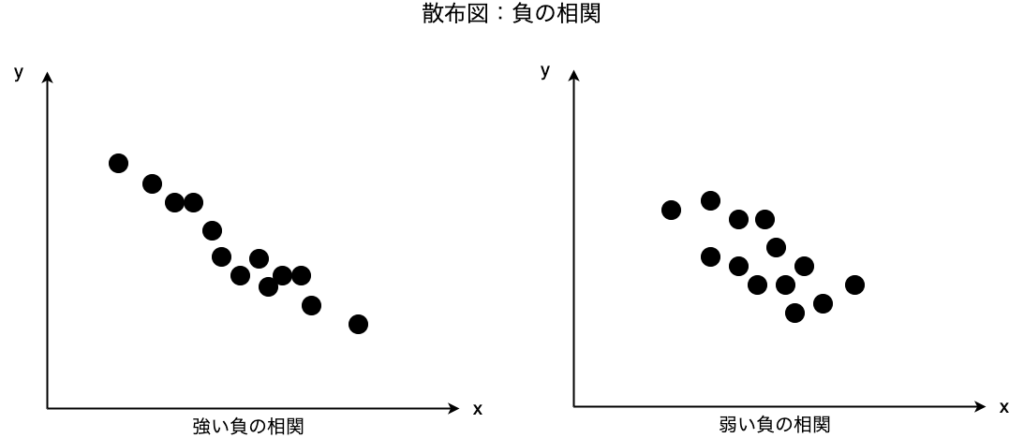
また、一方のデータが増大しようが減少しようが、もう一方のデータには関わりがない関係を無相関といいます。このとき相関係数は0に近い値となります。
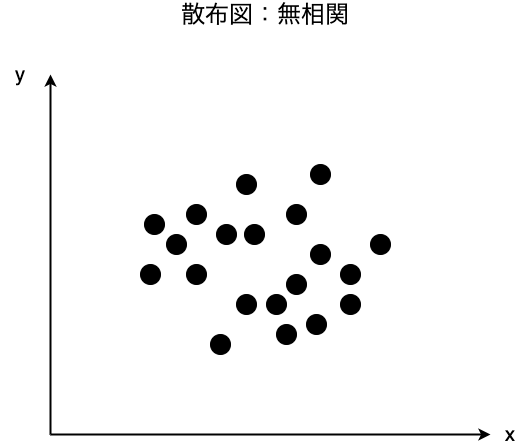
一般的には、相関係数が0.7以上であれば強い正の相関、ー0.7以下では強い負の相関、ー0.2〜0.2の値であればほとんど相関がないといって良いです。
また、相関係数とは別に決定係数というものもあります。
こちらは相関係数の2乗をとった値で$r^2$とあらわされます。
決定係数は0〜1までの値をとり、1に近ければ2つのデータが直線関係、0に近ければ直線ではない関係であることを示します。
この値はよくExcelの散布図に近似線を描くとき「R-2乗値」として表現される値なので、覚えておきましょう!
以上が相関係数の概要と相関との関係についてです。次はいよいよ相関係数の計算方法について解説します。
相関係数の計算方法(定義式からの計算)

相関係数は、それぞれ2変数の共分散をそれぞれの変数の標準偏差をかけ合わせた値で割ることで求めることができます。
具体的には、2つの変数を$x, y$としたときに、2変数の共分散を$s_{xy}$、それぞれの標準偏差を$s_{x}, s_{y}$としたときに、相関係数$r$は以下の式であらわします。
$$ 相関係数:r = \frac{s_{xy}}{s_{x} \times s_{y}} $$
2つのデータの共分散$s_{xy}$は、2つの変数$x, y$とそれぞれの平均値$\bar{x}, \bar{y}$、データの値を$x_{i}, y_{i}$、データの個数を$n$としたときに以下の計算式であらわすことができます。
$$ 共分散:s_{xy} = \frac{1}{n} \sum_{i=1}^{n} (x_{i} – \bar{x})(y_{i} – \bar{y}) $$
また、それぞれの変数の標準偏差$s_{x}, s_{y}$は、先ほどの平均値、データの値、データの個数を使って以下の式で計算できます。
$$ 変数 x の標準偏差:s_{x} = \sqrt{ \frac{1}{n}\sum_{i=1}^{n} (x_{i} – \bar{x})^2 } $$
$$ 変数 y の標準偏差:s_{y} = \sqrt{ \frac{1}{n}\sum_{i=1}^{n} (y_{i} – \bar{y})^2 } $$
数式だと少しわかりづらいと思いますので、具体的な計算手順をまとめると以下となります。
- それぞれの平均値・分散・標準偏差を計算する
- それぞれの変数データの偏差を計算しかけ合わせる
- かけ合わせた偏差の平均値を計算する(共分散の計算)
- 共分散をそれぞれのデータの標準偏差をかけ合わせた値で割る
では、具体的な事例を使って相関係数を計算してみましょう!
ある5人の身長と体重のデータがある。このときの身長と体重の相関係数を計算せよ。
身長と体重のデータは以下である。
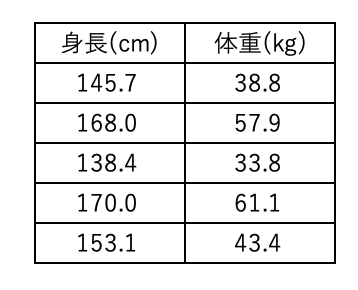
まずは、相関係数がどのような値になるか予測するために、2変数のデータを散布図であらわします。
身長を横軸、体重を縦軸として散布図を作成すると以下のようになります。
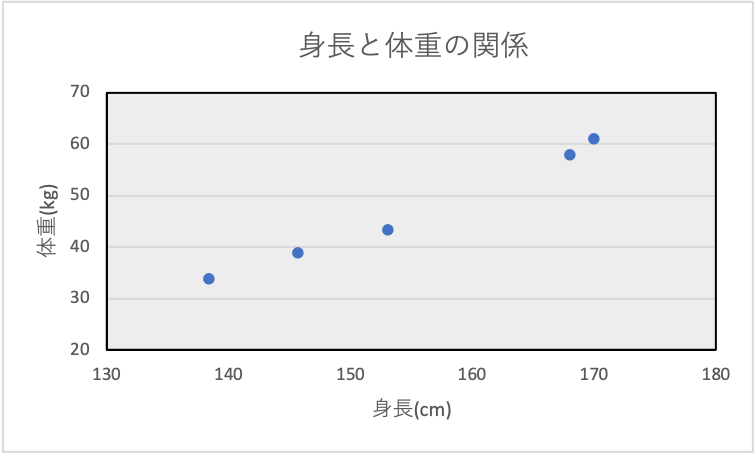
身長と体重の散布図を見るとおおむね右肩上がりの関係、すなわち身長が大きくなると、体重も大きくなることがわかります。
よって、相関係数の値は1に近い値である可能性が高いと予測できます。
データの散布図を作成したら、次は相関係数を計算するためにまずは身長・体重の平均値・分散・標準偏差を計算します。
平均値はデータの合計をデータの数で割ることで計算できます。
よって、身長と体重の平均値は以下のようになります。
$$ 身長の平均値:\bar{x} = \frac{145.7+168.0+138.4+170+153.1}{5} = 155.0 $$
$$ 体重の平均値:\bar{y} = \frac{38.8 + 57.9 + 33.8 + 61.1 + 43.4}{5} = 47.0 $$
次に分散および標準偏差を計算します。
分散は、データと平均値の差(偏差)の2乗してその平均値を計算してあらわすことができます。
よって、身長と体重の分散は以下のようになります。
$$ \begin{eqnarray}
身長の分散:s_{身長}^2 &=& \frac{(145.7-155.0)^2+(168.0-155.0)^2+ \cdots +(153.1-155.0)^2}{5} \\
&=& \frac{(-9.3)^2 + (13.0)^2 + (-16.0)^2 + (15.0)^2 + (-1.9)^2}{5} \\
& \fallingdotseq & 151.9 \\
\end{eqnarray} $$
$$ \begin{eqnarray}
体重の分散:s_{体重}^2 &=& \frac{(38.8-47.0)^2+(57.9-47.0)^2+ \cdots +(43.4-47.0)^2}{5} \\
&=& \frac{(-8.2)^2 + (10.9)^2 + (-13.2)^2 + (14.1)^2 + (-3.6)^2}{5} \\
& \fallingdotseq & 114.4 \\
\end{eqnarray} $$
標準偏差は、分散の平方根をとることで計算できます。
よって、身長と体重の標準偏差は以下のようになります。
$$ 身長の標準偏差:s_{身長} = \sqrt{151.9} = 12.33 $$
$$ 体重の標準偏差:s_{体重} = \sqrt{114.4} \fallingdotseq 10.70 $$
以上が、平均値・分散・標準偏差の計算となります。
身長と体重の平均値・分散・標準偏差を計算したら、それぞれのデータの偏差を計算しかけ合わせます。
偏差はデータと平均値の差で計算でき、それらをかけ合わせると以下のようになります。
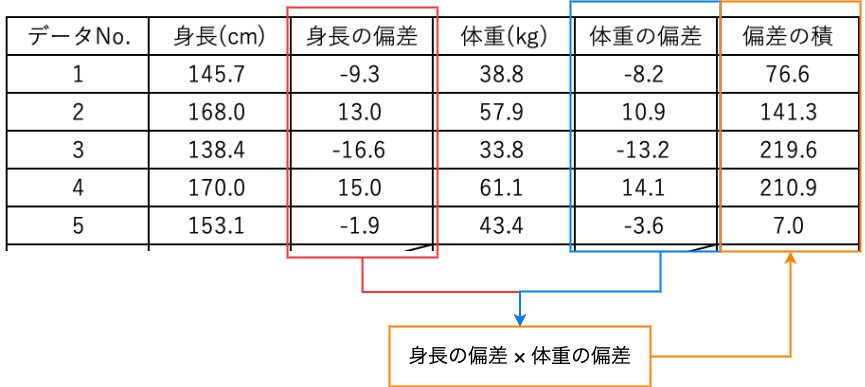
身長と体重の偏差をかけ合わせたら、この値の平均値を計算します。この値を共分散といいます。
平均値は合計した値をデータの数で割ることで計算できるので以下のように求めることができます。
$$ 共分散:s_{身長 \times 体重} = \frac{76.6 ; 141.3 + 219.6 + 210.9 + 7.0}{5} = 131.08 $$
よって身長と体重の共分散は131.08となります。
最後に先ほど計算した共分散と、身長と体重の標準偏差を使って相関係数を計算します。
相関係数は、共分散を身長と体重の標準偏差をかけ合わせた値で割ることで計算できます。
$$ \begin{eqnarray}
相関係数:r_{身長 \times 体重} &=& \frac{s_{身長 \times 体重}}{s_{身長} \times s_{体重}} \\
&=& \frac{131.08}{12.33 \times 10.70} \\
& \fallingdotseq & 0.994 \\
\end{eqnarray} $$
よって、身長と体重の相関係数は0.994と計算できました。
この値から身長と体重の関係は強い正の相関、すなわち身長が大きければ体重も大きくなる関係であることがわかりました。
以上が相関係数の計算方法になります。しかし非常に手間がかかると感じる人もいるかもしれません。
そこで最後にExcelを使った相関係数の計算方法について解説します。
相関係数の計算方法(Excelを使った計算方法)

相関係数を計算するためのExcelの関数は以下の通りです。
$$ = \mathrm{ CORREL }(配列 1, 配列 2) $$
たとえば、以下のExcelシートのように身長のデータをC27〜C31、体重のデータをD27〜D31にまとめたとします。
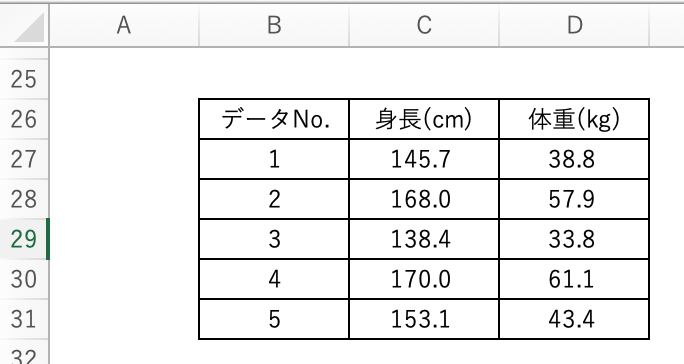
このとき、相関係数を計算する場合、以下のように関数を適用します。
$$ = \mathrm{ CORREL(C27 : C31, D27 : D31) } $$
以上のように関数を組み込むことで相関係数を計算することができます。
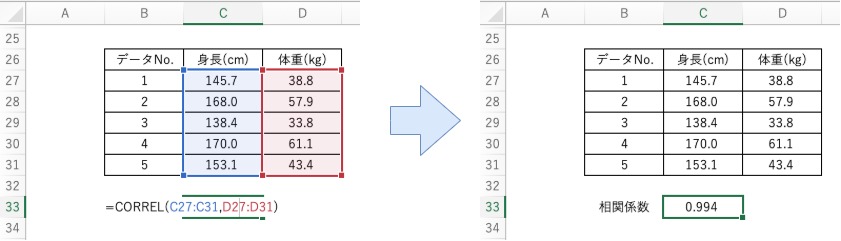
相関とは 相関・相関係数の基礎から 計算方法まで徹底解説:まとめ
いかがでしたでしょうか?以下まとめです。
- 相関とは、2つのデータの直線的な関係
- 相関の強さをあらわす統計量を相関係数
- 相関係数は2つのデータの共分散からそれぞれのデータの標準偏差で割ることで計算できる
- Excelでは$=\mathrm{CORREL}$(配列1, 配列2)を使って計算することができる
みなさんもぜひ相関や相関係数を理解し、2つのデータの関係について理解できるようにしましょう!
より高度な統計学を勉強したい方へ
この記事を読んで、共分散を使った統計学(回帰分析や相関)について勉強したいと思った方は「入門 統計解析法」がおすすめです。
この本では、分散や標準偏差などの基本的内容から仮説検定・分散分析・回帰分析といった製造業の現場で実践的に使える統計学について学ぶことができます。
高校数学の内容までの数式を使いますが、実際の製造業で使われる具体例を用いて統計学を解説しておりますので、使い方をイメージできる一冊となります。
特に先ほど紹介した共分散についてや、共分散を相関・回帰分析に活用している例が記載されております。
数学の知識を持っており、実務で使える本格的な統計学を学びたい方にはぜひおすすめの本です!
みなさんもぜひ統計学の勉強にチャレンジし、ビジネスで活用できるようになったら幸いです。
最後までのこの記事を読んでいただきありがとうございました!
統計学を動画で勉強したい方はこちら! ![]()





コメント