こんにちは、かじつとむです。
前回、統計学に必要な確率について説明しました。
今回は、確率を計算するために必要な場合の数、順列やその応用である階乗について解説します。
この記事を読むことで、以下のことがわかります。
- 順列と階乗について理解することができる
- 順列と階乗の計算方法について理解することができる
それでは、いってみましょう!
場合の数とは(復習)

場合の数とは、ある現象が起こるすべての場合の総数のことをいいます。
たとえば、コインを1枚投げたときの場合の数は表と裏がありますので、合計で2となります。
また、サイコロを1つ投げたときの偶数の目がでる場合の数は、2の目と4の目と6の目がありますので、合計で3となります。
このように起こりうるすべての可能性を数えた総数を場合の数といいます。
場合の数を数えるには、注意点があります。それは、「同様に確からしい」ものを数えることです。
同様に確からしいとは、起こる可能性が同じであることをいいます。
たとえばサイコロを1回振ったときに出る目の数は、1の目、2の目、3の目、4の目、5の目、6の目が同じ可能性で起こります。
このように1つ1つの現象を区別することで、同様に確からしいことを満たして場合の数を数えることができます。
場合の数の数え方を理解したところで、次は具体的にどのような場合の数の1つである順列について解説します。
場合の数:順列とは 意味と計算方法

順列とは、異なるn個のものからr個を選んで並べる場合の数のことをいいます。
ここでいうnとrは任意の数字でありますが、nの数字がrの数字を超えることはありません。
順列が使われる例について説明します。
A, B, C, D、4人のうち3人を選んで並べるときの場合の数は?
まずは、場合の数を樹形図を使って数えてみます。
樹形図とは、ものごとを順番に書き出して数える方法です。
先ほどの4人のうち3人を並べるときの樹形図は次のようになります。
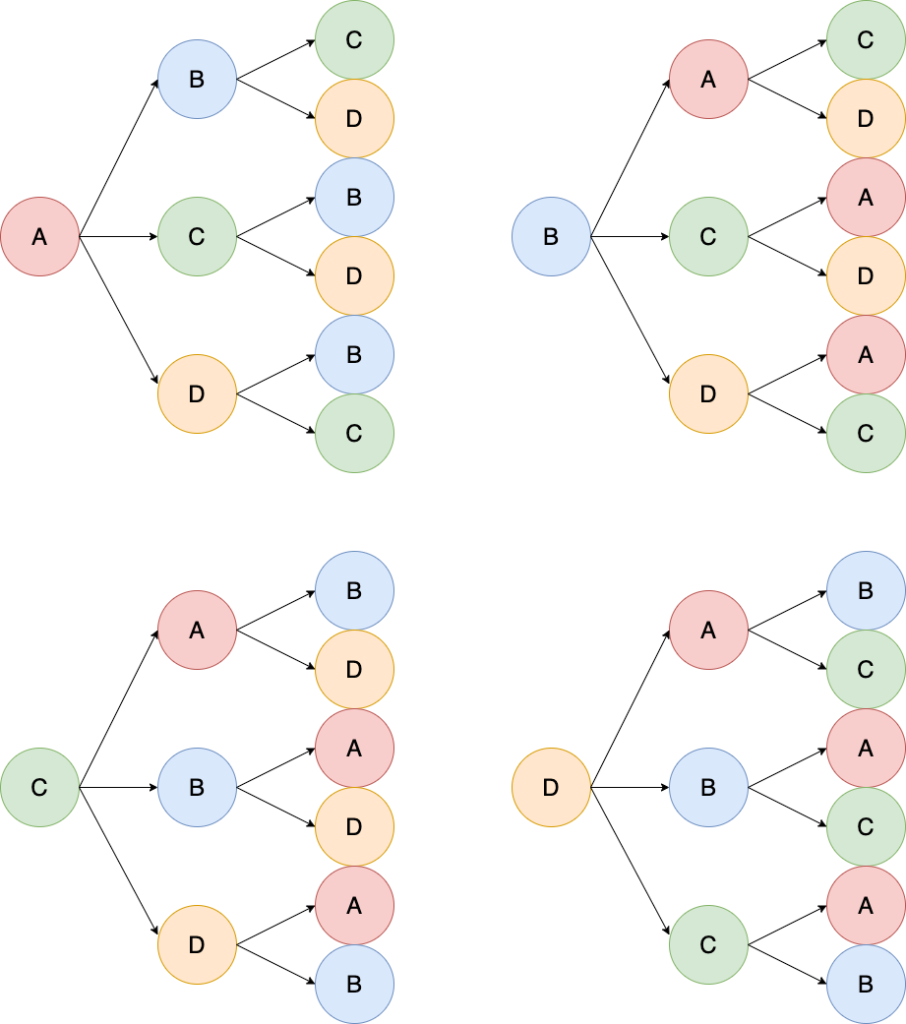
このように樹形図で表すことで、4人から3人を選んで並べるときの場合の数すべてを表すことができます。
そしてこの場合の数は24通りであることがわかります。
しかし、選ぶ数が5人、6人と増えていくと樹形図を書いて数えるのは大変になります。
ですので、どんな個数や人数であっても数えられるように場合の数には計算式があります。
n個のものからr個を選んで並べる場合の数(順列)を計算するための式は以下の通りになります。
$$ {}_n \mathrm{ P }_r = n \times (n-1) \times (n-2) \times \cdots \times (n-r+2) \times (n-r+1)$$
n個のものからr個を選んで並べる場合の数を計算する場合、まずはn個すべてに対して可能性がありますので、nをかけます。
次に、n個から1個を取り除いた$ n – 1 $個に対して可能性がありますので$ n – 1 $をかけます。
さらに、n個から2個を取り除いた$ n – 2 $個に対して可能性がありますので$ n – 2 $をかけます。
この作業をr回繰り返し、r回目に$ n-r+1 $をかけるとn個のものからr個を選んで並べたときの場合の数(順列)を計算することができます。
では、先ほどの例で4人から3人を選んで並べるときの場合の数を計算してみましょう!
- 最初に4人いるので4パターン可能性があるので4をかける
- 次に3人いるので3パターン可能性があるので3をかける
- 最後に2人いるので2パターン可能性があるので2をかける
これらを順列の式に当てはめると以下のようになります。
$$ {}_4 \mathrm{ P }_3 = 4 \times 3 \times \ 2 = 24通り$$
樹形図で数えた値と同じ24通りを計算で出すことができました。
また、順列をあらわすときのPはpermitation(パーミテーション)の略で、この単語は順列・交換・並べ替えという意味があります。
場合の数:階乗とは 意味と計算方法

順列と似たような場合の数で階乗があります。
階乗とは、1からある数までの整数の積のことをいいます。
たとえば、nの階乗の場合は1からnまでの整数の積で、以下のようにあらわします。
$$ n! = n \times (n-1) \times (n-2) \cdots \times 2 \times 1 $$
また、順列の式を使うとnの階乗は以下のようにあらわすことができます。
$$ n! = n \times (n-1) \times (n-2) \cdots \times 2 \times 1 = {}_n \mathrm{ P }_n$$
nの階乗を${}_n \mathrm{ P }_n$であらわすことができます。
すなわち、nの階乗はn個のものをすべて並べたときの場合の数であることを示しております。
確率に必要な場合の数(順列):まとめ
いかがでしたでしょうか?以下まとめです。
- 順列とは、異なるn個のものからr個を選んで並べる場合の数をさす
- 階乗とは、1からある数までの整数の積のことである
- nの階乗は、1からnまでの整数の積であり、n個のものをすべて並べたときの場合の数でもある
みなさんも、場合の数を理解して確率の理解の一歩を踏み出してみてください!
確率や統計を勉強したい方へ

統計学に必須の確率の基礎知識について勉強したい方は「ふたたびの確率・統計[1]確率編」がおすすめです。
この本は、統計学に必要な集合や場合の数、確率について理解するのにおすすめの書籍となります。
集合や場合の数、確率についてはわかりやすく、かつ、数学的な用語についても網羅的に学ぶことができます。
本の巻末には、大学入試問題を使った腕試しもできるので、高校生にとってもおすすめの書籍となります。
数学の用語等も図解でわかりやすく、かつ丁寧に解説しておりますので、中学や高校生のときに数学が苦手だった方でもとっつきやすい本となります。
もしこの本で勉強したい方がいれば、ぜひ以下のリンクからどうぞ!
みなさんもぜひ確率について勉強してみましょう!
最後までこの記事を読んでいただきありがとうございました!
統計学からデータサイエンスについて動画で勉強したい方はUdemyの「【世界で37万人が受講】データサイエンティストを目指すあなたへ〜データサイエンス25時間ブートキャンプ〜」がおすすめ!





コメント