こんにちは、かじつとむです。
みなさんは基本統計量ってご存知でしょうか?
あまりききなれない言葉ですが、基本統計量を理解することでデータの特徴を簡単に表すことができます。
そんな便利な基本統計量について説明したいと思います。
この記事を読むことで以下のことがわかります。
- 基本統計量の概要について知ることができる
- 基本統計量の代表である平均値、分散、標準偏差の意味や求め方を理解できる
それではいってみましょう!
基本統計量について:基本統計量とは
基本統計量とは、データ分布の特徴を1つの数値で表す指標のことです。
つまり、データの基本統計量がわかれば、どんなデータであるのか、1つの数値に偏りがあるのか、数値の信憑性はどうかを理解することができます。
では、基本統計量はどのようなものなのか代表的なものを図でまとめます。
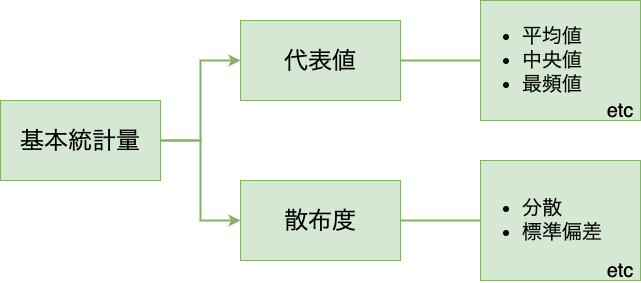
基本統計量は、代表値と散布値の2つから構成されています。
代表値とは、データを代表するような値であり、平均値・中央値・最頻値などが挙げられます。
散布値とは、データがどのくらい散らばっているかを示す指標であり、分散・標準偏差などが挙げられます。
では、次に基本統計量を代表する3つの値、「平均値」「分散」「標準偏差」について説明します。
この3つが理解できれば、ほとんどのデータに対して考察できるようになります。
基本統計量について:その1 平均値
平均値はデータの合計をデータの数で割ることで得られる値です。
これは誰でも理解していることだと思います。
では、平均値を表す意味はなんでしょうか?その答えについて以下の図で示します。
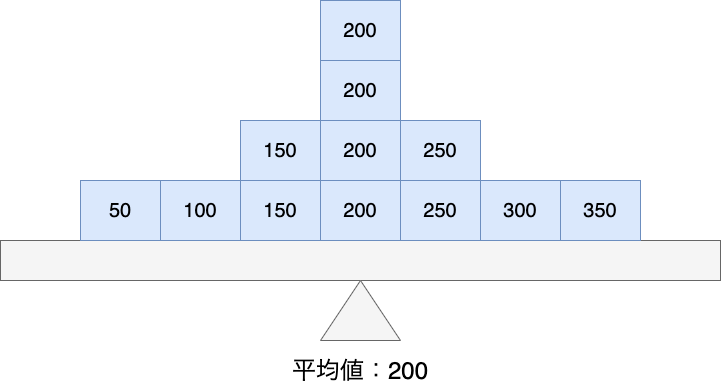
上の図は50〜350までの数値データが12個あります。このデータを合計すると2400になり、これをデータの個数である12個で割ると平均値200を得ることができます。
ここで重要なのは、平均値はデータの広がりの中にある1点を選び出したものであることです。
上の図では一番小さいデータが50で一番大きなデータが350であるが、これらの値よりも外側の値を平均値がとることはありません。したがって、平均値は必ずデータの範囲内にあります。
平均値を数式から考えるとすべてのデータを集めて均等にわけた値となります。
言い換えるとデータの中心的な値が平均値となります。また、データはすべて平均値の周辺に分布しているともいうことができます。
ここで1つ注意があります。それは、必ずしもデータは平均値に近しい値をとるわけではないということです。これについて次の図で説明します。
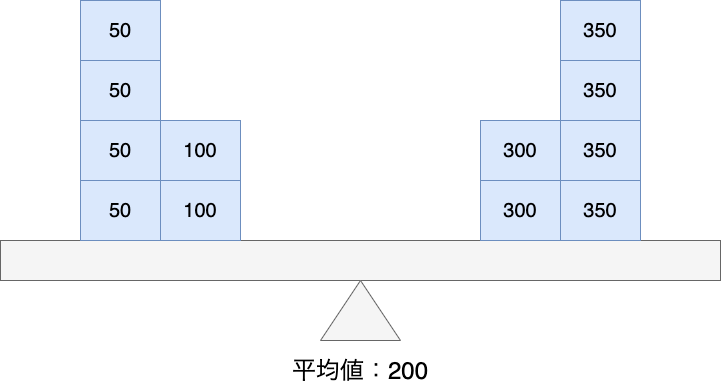
上の図は、50と350のデータがそれぞれ4つ、100と300のデータがそれぞれ2つ、合計で12個のデータがあります。これらのデータの合計は2400であり、データの個数である12個で割ると平均値は200となります。
ここで注目すべき点は平均値200に対して近しい値がないということです。
すなわち、平均値はデータの中心的な値ではあるが、平均値そのものがデータを完全に表しているわけではないということです。
では、平均値だけでは説明できないデータの場合どのように表せば良いのでしょうか。そこでデータの散らばり具合を表現する基本統計量、分散や標準偏差の出番となります。まずは分散について説明します。
基本統計量について:その2 分散
分散とは、データのばらつき具合を評価できる指標となります。計算式は以下となります。$$分散 = \frac{(データと平均値の差)^2の合計}{データの数}$$まず、すべてのデータに対して平均値との差をとります。(これを偏差といいます) 次にこの値を2乗し、その合計をもとめます。最後に、この合計をデータの数で割ると分散になります。
具体例として、先ほど図で示した2つのデータについて分散を計算してみましょう。
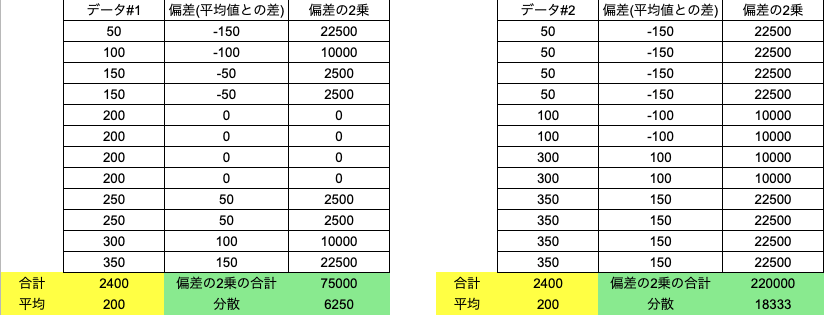
最初の図のデータをデータ#1、次の図のデータをデータ#2として表しました。データ#1の分散は6250に対して、データ#2の分散は18333となります。これは、データ#1よりもデータ#2の方がばらついていることがわかります。
ところで、なぜ分散は偏差の2乗をしなければならないのでしょうか?
これは、データと平均値の差の大きさをもとめたいからです。
本来データと平均値の差は正の値と負の値それぞれとります。この差をそのまま合計すると正の値と負の値が打ち消しあって0になってしまいます。このままだとデータと平均値の差の比較をすることはできません。
そこでデータと平均値の差を2乗することで、すべての値が正の値となり、その合計した値で大きさを比較することが可能になります。
しかし、この分散をそのままばらつきの具合として表現することはできません。
これには2つの理由があります。
まず、ばらつき具合の大きさが大きすぎる点が挙げられます。#1、#2のデータはどちらも平均値に対して±150の範囲におさまっておりますが、分散は6250と18333であるため比較対象にするには大きすぎます。
もう1つの理由は、単位が変わってしまっている点が挙げられます。
これはデータの値が長さのmだとしたら、分散の単位はm2となっています。
これだと、単位が異なるため平均値やデータと比較することができません。
これら2つの問題点を解決するために標準偏差が必要になります。次は標準偏差について説明します。
基本統計量について:その3 標準偏差
標準偏差とは、分散の平方根をとった値のことをいいます。計算式を以下に示します。$$標準偏差 = \sqrt{分散}$$分散の平方根をとった標準偏差は2乗された単位は元に戻り、平均値やデータに対して比較することができるようになります。
具体例として、先ほどのデータ#1とデータ#2の標準偏差をもとめてみましょう。データ#1とデータ#2の分散はそれぞれ6250と18333であるため、この値の平方根をとるとおおよそ79と135となります。
これは、データ#1では平均値は200であるがその前後に約79ほど数値がばらつくことを示しています。同じくデータ#2ではデータ#1と同様、平均値は200であるがその前後に約135ほど数値がばらつくことを示しています。これらの結果よりデータ#2はデータ#1と比べると約2倍ばらつくことがわかります。
標準偏差を使った解析方法は他にもあります。
たとえば、製造業では工程能力という指標を使って品質管理を行なっています。
工程能力は求めたい品質の標準偏差と平均値を計算し、求めることができます。
工程能力での解析方法について知りたい方は以下のリンクからどうぞ!
このように平均値・分散・標準偏差を組み合わせてデータを解析します。
基本統計量について:まとめ
今回は基本統計量について説明しました。以下まとめです。
- 基本統計量とは、データ分布の特徴を1つの数値で表す指標である。
- 基本統計量は、データを代表する代表値とデータのばらつき具合を示す散布値で構成される。
- 平均値とは、データの中心的な値であるが必ずしもそのデータに近しい値を取るわけではない。
- 分散とは、データのばらつき具合を評価する指標。ただしデータや平均値との比較はできない。
- 標準偏差とは、分散の平方根をとった値。標準偏差にすることでデータや平均値と比較することができる。
以上です。みなさんも平均値だけではなく、そのばらつきを示す分散や標準偏差についても検討しながらデータ分析を進めてみましょう!
統計学をもっと勉強したい方へ
統計学を初めて学ぶおすすめの書籍を紹介します。入門者におすすめなのは「完全独習 統計学入門」です。
この本では、データの特徴をあらわす記述統計学からデータの予測をする推測統計学まで一通り勉強することができます。
具体的には、先ほど勉強したヒストグラムや平均・分散・標準偏差といった基本統計量の使い方、さらには統計量を推定する方法を勉強できます。
この本の特徴は、難しい数学や数式をほとんど使うことなく統計学を勉強することができます。
また、各講ごとに練習問題もありますので、こちらを解くことで統計学を体感することもできます。
統計学を初めて勉強したいと思った人や数学が苦手だけど統計学を学びたい方には、おすすめの一冊となります。
もしよろしければ、以下のリンクからどうぞ!
ぜひ、統計学を勉強してさまざまなビジネスシーンに活かせるように勉強していきましょう!
最後までこの記事を読んでいただきありがとうございました!
統計学を動画で勉強したい方はこちら!





コメント