こんにちは、かじつとむです。
今まで、標本から母集団を推定する方法について解説してきました。
今回は、母集団に関する仮説をデータを用いて検証する仮設検定について解説します。
この記事を読むことで、以下のことがわかります。
- 仮説検定とはどういうものなのか理解できる
- 仮説検定に使う用語について理解できる
- 仮説検定のやり方について理解できる
それではいってみましょう!
仮説検定とは
仮説検定とは、母集団に関する仮説を標本のデータを用いて検証する方法です。
たとえば、サイコロを振ったときに1回目に1の目が出たとします。この現象は普通の現象です。
続けて2回、3回、4回、5回とサイコロを投げて1の目が出続ける場合と、この現象はおかしいと考えはじめます。
このとき、仮説として「サイコロは正しい」とした場合、サイコロを5回投げて5回連続で1の目が出続ける確率を計算します。そして、この確率がある一定以上小さければ「サイコロは正しい」という仮説を排除していきます。
このように仮説を立てて、その仮説が正しいという前提で標本のデータが得られる確率を計算します。この確率の結果を検証し、仮説が正しいのか間違っているのかを検証する方法が仮説検定です。
仮説検定の概要がわかったところで、次は仮説検定で使用する用語について解説します。
仮説検定で使用する用語
仮説検定で使用する用語は以下の4つになります。
- 帰無仮説と対立仮説
- 検定統計量
- 有意水準
- 棄却と採択
それぞれの用語について解説します。
仮説検定で使用する用語 その1:帰無仮説と対立仮説
帰無仮説とは、自分が否定したい仮説のことをいいます。
一方で対立仮説は、自分が考えたり感じたりした仮説のことをいいます。
たとえば、5回連続で1の目が出たときにこのサイコロは正しいものではないと考えます。
このとき、帰無仮説は「サイコロは正しい」ということになり、対立仮説は「サイコロは正しくない」となります。
なぜならば、5回連続で1の目が出たときに自分が感じたことは「サイコロは正しくない」ということで、否定したいことは「サイコロは正しい」ということだからです。
また、帰無仮説を$H_{0}$、対立仮説を$H_{1}$と記号を使って表記します。
よって、先ほどのサイコロの例は仮説検定において以下のように書くことがあります。
- 帰無仮説 $H_{0}$:サイコロは正しい
- 対立仮説 $H_{1}$:サイコロは正しくない
上記のように帰無仮説と対立仮説を立ててどちらが正しいのかを判断していきます。これが仮説検定です。
仮説検定で使用する用語 その2:検定統計量
検定統計量とは、検定するために使用される値のことをいい、統計量とも呼ばれます。
検定統計量には、いろんな種類がありますが今回は代表的な2つの検定統計量について解説します。
それは統計量$z$と統計量$t$です。
統計量$z$とは平均が0、分散が1となるように標本データを標準化した値です。
統計量$z$は母集団の情報として、母平均$\mu$と母分散$\sigma^2$がわかっているときに使われます。
統計量$z$は、母平均$\mu$、母分散$\sigma^2$、標本平均$\bar{x}$、標本データの数$n$を用いて以下のように計算します。
$$ 統計量 z = \frac{ \bar{x} – \mu }{ \sqrt{ \frac{ \sigma^2 }{n} } } $$
この統計量$z$を使って仮設検定を行う場合は、標準正規分布を使用します。
標準正規分布についてもっとよく知りたい方は以下のリンクからどうぞ!
統計量$t$も同じく平均が0、分散が1となるように標本データを標準化した値です。
ただし、統計量$t$は母集団の情報として、母平均$\mu$だけがわかっているとき、すなわち母分散$\sigma^2$がわからないときに使われる統計量です。
統計量$t$は、母平均$\mu$、標本平均$\bar{x}$、標本データの数$n$、そして標本データから得られる不偏分散$U^2$を用いて以下のように計算します。
$$ 統計量 t = \frac{ \bar{x} – \mu }{ \sqrt{ \frac{ U^2 }{n} } } $$
この統計量$t$を使って仮設検定を行う場合は、t分布を使用します。
t分布についてもっとよく知りたい方は以下のリンクからどうぞ!
検定統計量は、母集団の情報や仮説の種類によってとりうる値が変わっていきます。
仮説検定で使用する用語 その3:有意水準
有意水準とは、帰無仮説に対して得られたデータが正しいかどうか判断する基準となる確率のことをいい、記号αであらわします。
有意水準は一般的に5%(0.05)や1%(0.01)といった値がよく使われます。
有意水準を5%に設定することは、「帰無仮説で5%以下で起こる確率の現象であり、この現象はとても珍しいため何かしらのおかしなことが起こった」ということをあらわします。
また、設定した有意水準は検定統計量によって従うべき確率分布が変化します。
たとえば、検定統計量が統計量$z$の場合、有意水準に対して標準正規分布という確率分布に従います。よって、統計量$z$の有意水準に対する値は標準正規分布表で得ることができます。
仮説検定で使用する用語 その4:棄却と採択
検定統計量が有意水準で与えられる基準から外れる場合、帰無仮説を棄却するといいます。
棄却というのは、ある内容を否定するという意味です。また、有意水準から外れる領域を棄却域といいます。
一方で、検定統計量が有意水準で与えられる基準内である場合、帰無仮説を採択するといいます。
採択というのは、ある内容を否定することはできないという意味です。
棄却域は有意水準だけでなく、対立仮説のとり方によって変化していきます。
たとえば、「部品寸法が変わっていない」という帰無仮説があった場合、以下の3つの対立仮説が考えられます。
- 部品寸法が変わっている
- 部品寸法が大きくなっている
- 部品寸法が小さくなっている
1つ目の「部品寸法が変わっている」という対立仮説の場合は両側検定で仮説検定を行います。
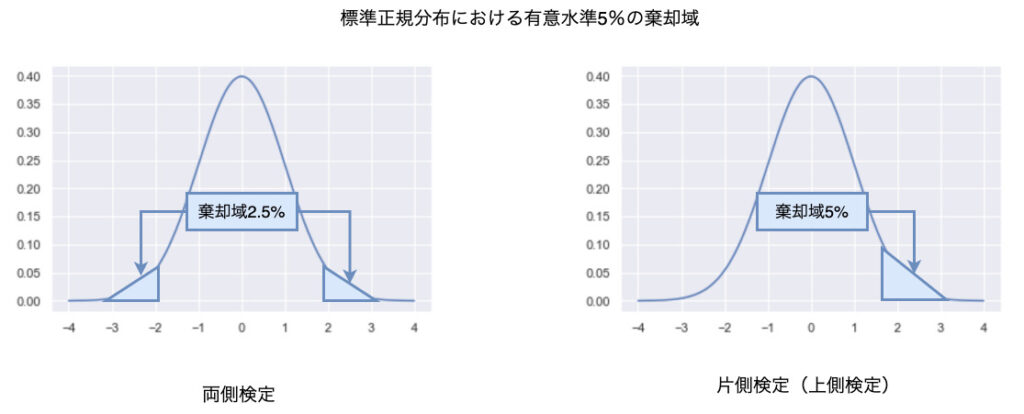
両側検定とは、両側に棄却域を設定して仮説検定を行います。これは有意水準を5%とした場合、上側2.5%と下側2.5%に棄却域を設定し、検定統計量がこの領域に存在するかどうかで仮説検定を行います。
2つ目の「部品寸法が大きくなっている」、3つ目の「部品寸法が小さくなっている」という対立仮説の場合は片側検定で仮説検定を行います。
片側検定とは、上側もしくは下側どちらかに棄却域を設定し仮説検定を行います。
「部品寸法が大きくなっている」という対立仮説の場合、有意水準を5%としたとき、上側5%に棄却域を設定し、この領域に検定統計量が存在するかどうかで仮説検定を行います。
一方で「部品寸法が小さくなっている」という対立仮説の場合、有意水準を5%としたとき、下側5%に棄却域を設定し、この領域に検定統計量存在するかどうかで仮説検定を行います。
以上が、仮説検定で使用する用語の解説でした。
用語がわかったところで次はいよいよ仮説検定の方法について解説します。
仮説検定の方法
仮説検定の方法は以下の手順で行います。
- 帰無仮説と対立仮説を設定する
- 有意水準を決める
- 母集団の情報から使用する確率分布と棄却域を決める
- 得られたデータから検定統計量を計算する
- 検定統計量と棄却域を比較し、帰無仮説を棄却するかどうか判断する
それぞれの手順について以下の例を用いて解説します。
ある工場で鉄の部品にピアス穴を開けている。開けているピアス穴の直径は母平均$\mu = 1.8$、母分散$\sigma^2 = 0.4^2$の母集団に従っている。最近のピアス穴のデータを見ると穴の大きさが変化しているのではないかと考えた。そのデータを以下に示す。
1.68、1.53、1.84、1.89、1.71、1.62、1.85、1.66、1.80、1.70
仮説検定の方法 その1:帰無仮説と対立仮説を設定する
まず、帰無仮説と対立仮説を設定します。
今回はピアス穴の大きさが変化しているのではないかということを感じでいますので、帰無仮説と対立仮説は以下のように設定します。
- 帰無仮説:ピアス穴の平均値が変わっていない
- 対立仮説:ピアス穴の平均値が変わっている
仮説検定の方法 その2:有意水準を決める
帰無仮説と対立仮説を設定したら、有意水準を決めます。
有意水準は一般的に5%か1%に設定します。
今回は有意水準を5%に設定します。
仮説検定の方法 その3:母集団の情報から使用する確率分布と棄却域を決める
有意水準が決まったら、母集団の情報から使用する確率分布を決めます。
今回は母平均と母分散が両方わかっているので、確率分布は標準正規分布を使用します。
有意水準と確率分布が決まったので棄却域を決めることができます。
確率分布は標準正規分布なので、標準正規分布表を使って棄却域を決めます。
また、有意水準は5%であることと、対立仮説が「ピアス穴の平均値が変わっている」ということから両側検定を使った棄却域を決めます。
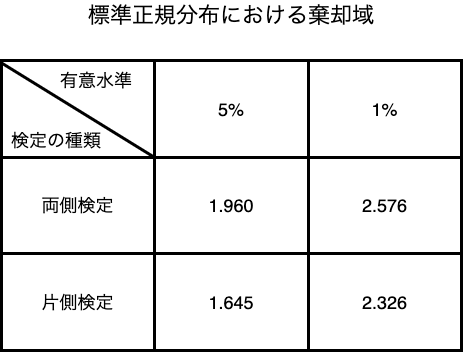
今回の棄却域は有意水準が5%での両側検定であるため、1.960となります。
仮説検定の方法 その4:得られたデータから検定統計量を計算する
棄却域が決まったら、得られたデータから検定統計量を計算します。
まず検定統計量は標準正規分布を使用しているため、統計量$z$を計算します。
よって、データから標本平均$\bar{x}$、標本データの数$n$を計算します。
標本平均は1.72、標本データの数は10となりますので、母平均1.8、母分散$0.4^2$も合わせて使うことで、統計量$z$は以下のように計算できます。
$$ \begin{eqnarray}
統計量 z = \frac{ \bar{x} – \mu }{ \sqrt{ \frac{ \sigma^2 }{n} } } \\
= \frac{1.72-1.8}{\sqrt{\frac{0.4^2}{10}}} \\
\fallingdotseq -1.265
\end{eqnarray}$$
よって検定統計量はー1.265となります。
仮説検定の方法 その5:検定統計量と棄却域を比較し、帰無仮説を棄却するかどうか判断する
検定統計量を計算したら棄却域と比較し、帰無仮説を棄却するかどうか判断します。
検定統計量と棄却域と比較し棄却される条件は以下となります。
$棄却される場合:検定統計量の絶対値 \geq (棄却域)$
今回の検定統計量はー1.265であり、棄却域は1.960であるため以下の関係となります。
$(検定統計量の絶対値)1.265 \leqq 1.960(棄却域)$
以上の関係より、棄却される場合の条件を満たさないため、帰無仮説を棄却できません。
すなわち、今回の「ピアス穴の大きさが変わっていない」という帰無仮説を採択します。
以上が仮説検定の方法となります。
【データから母集団を検証する】仮説検定とは:まとめ
いかがでしたでしょうか?以下まとめです。
- 仮説検定とは、母集団に関する仮説を標本のデータを用いて検証する方法
- 仮設検定の方法は、「帰無仮説と対立仮説を設定する」「有意水準を決める」「母集団の情報から使用する確率分布と棄却域を決める」「得られたデータから検定量を計算する」「検定統計量と棄却域を比較し、帰無仮説を棄却するかどうか判断する」という5つを順番に行う
みなさんも、この記事を読んでぜひ仮説検定を理解し、仮説検定にチャレンジしてみてくださいね!
統計学をもっと勉強したい方へ
仮説検定を含めた統計学をもっと勉強したい方は「完全独習 統計学入門」と「入門 統計解析法
」の本がおすすめです。
「完全独習 統計学入門」では統計学について右も左もわからない人に向けて、統計学ってだいたいこういうものだよっというのがわかる本です。
ヒストグラムや統計量から区間推定まで網羅的に理解することができる本です。
図解でわかりやすく説明していることもさることながら、難しい数式をまったく使わないように配慮のある本となっております。
また、各章の最後には演習問題もありますので自然と統計学が身につくような設計の本となっております。
統計学をはじめて勉強する人がまず手に取って欲しい本となっております。
もう1つの「入門 統計解析法」は、「完全独習 統計学入門
」の次に統計学を勉強するのにおすすめの本です。
「入門 統計解析法」では、「完全独習 統計学入門
」で手が届かない詳しい内容や仮説検定・分散分析・回帰分析といったより実務に使える統計学について学ぶことができます。
こちらは、高校数学の内容までの数式を使いますが、とても丁寧に詳しく統計学を勉強できます。
「完全独習統計学」を読んでもっと高度な統計学を勉強したい方や、実務で使える本格的な統計学を学びたい方にはぜひおすすめの本となっております。
みなさんもぜひ統計学の勉強をしていってみましょう!
最後までこの記事を読んでいただきありがとうございました!








コメント