こんにちは、かじつとむです。
今まで統計学の記事において、さまざまな確率分布(標準正規分布やt分布など)を使って、データを推定する方法や検定をする方法について解説してきました。
この確率分布は統計学の基礎になる一方で、なんだか難しそうとかわからないという声があるかと思います。
今回は、そんな統計学の基礎となる確率分布について解説します。
この記事を読むことで以下のことがわかります。
- 確率分布について理解することができる
- 確率分布の種類について理解できる
それではいってみましょう!
【統計学で使う確率を理解する】確率分布とは
確率分布を説明する前にまずは確率変数について説明します。
確率変数とは、ある事象に対してどのような確率をとるのか決まっているという性質を持っている変数のことをいいます。
たとえば、コインを1回投げたときの表と裏が出る確率はそれぞれ1/2となります。この確率に対しての確率変数はコインの表、コインの裏となります。
$$確率変数:x = \{ 表, 裏 \} $$ $$確率:Pr\{x = 表\} = \displaystyle \frac{1}{2}, Pr\{x = 裏\} = \frac{1}{2}$$
そして、確率変数がどのような値になるか法則性があるものを確率分布もしくは分布といいます。
データ分析でいうならば、確率変数はデータのとりうる値で、確率分布はデータの値に対してどのくらいの確率になるか法則性を持ったものとなります。
以上が確率分布および確率変数についての概要です。
【統計学で使う確率を理解する】確率分布の種類
確率分布には以下のように2つの種類があります。
- 離散分布
- 連続分布
それぞれの確率分布について解説します。
確率分布の種類 その1:離散分布
離散分布は、確率変数1つ1つに対してそれぞれ確率が存在する確率分布です。
たとえば、コインを1回投げたときの表裏の確率や、サイコロ1回振ったときの1〜6までの確率などが離散分布となります。
離散分布を$ f_{i} $とすると、確率変数$x_{i}$の確率$Pr$は以下のようにあらわします。
$$ 離散分布:f_{i} = Pr\{x = x_{i}\} (i = 1, 2, ・・・) $$
また、離散分布には以下の性質があります。
$$ 0 \leq f_{i} \leq 1 (i = 1, 2, ・・・) $$ $$ \displaystyle \sum_{i=1}^{\infty} f_{i} = 1 $$
$ 0 \leq f_{i} \leq 1 $は離散分布は必ず0以上1以下の値をとるということです。
これは、確率がマイナスになることや、1より大きくなることもないということを示しています。
たとえば、1〜6の目が書いてあるサイコロを1回振った場合を考えてみましょう。サイコロを1回振ったとき、1〜6までの目が出る確率は1となります。これが1〜100までの目が出る確率も1となります。
では、7〜100までの目が出る確率はいくつでしょうか。
答えは、0となります。
なぜなら、起こり得ない事象の確率はすべて0として考えるためです。
よって、確率は0よりも下回ることはないですし、1よりも大きくなることもないのです。
$ \displaystyle \sum_{i=1}^{\infty} f_{i} = 1 $というのは離散分布をすべて足し合わせると、その合計は1となることです。
$ \displaystyle \sum_{i=1}^{\infty} f_{i} $は$fi$という離散分布に対して1から$\infty$までのとりうる値を合計するという意味です。
この値が1となるというのは、どれだけの確率があろうとその確率の合計は必ず1となることを示しています。
たとえば、コインを1枚投げたときの確率を考えてみましょう。コインの表が出る確率は1/2となりますし、裏が出る確率も1/2となります。そして、表と裏以外がでる確率は0です。
よってコインを1枚投げたときの確率は1/2 + 1/2 + 0 = 1となります。
このように事象に対するすべての確率を足し合わせると1となります。
以上が離散分布の解説となります。
確率分布の種類 その2:連続分布
連続分布は、確率変数が連続的な値をとるときにその確率の状態をあらわす確率分布です。
そしてこの連続分布がデータ分析を行うためによく使われます。
たとえば、あるデータのヒストグラムを考えてみましょう。
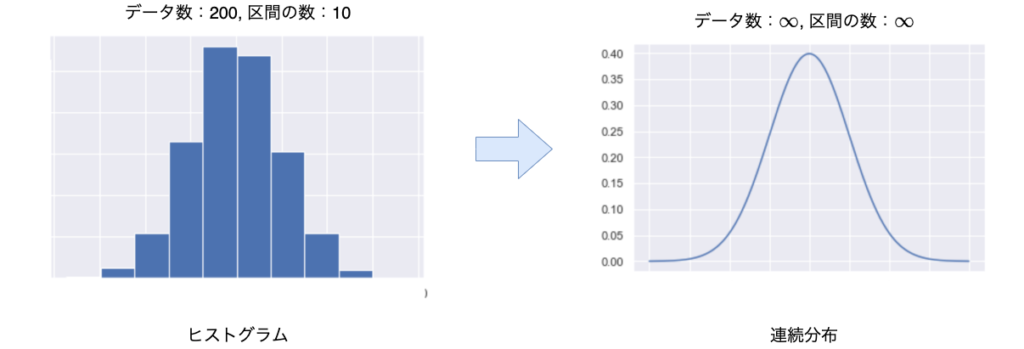
ヒストグラムとは、あるデータを特定の範囲に区切り、そのデータの個数を棒グラフであらわしたものです。
たとえば、データの個数を200にし、それを10個の区間でわけて、その区間に適応するデータの数を棒グラフであらわします。
このヒストグラムのデータの数と区間の数を無限にするとどうなるのでしょうか?
答えは、ヒストグラムの輪郭はどんどんなめらかな曲線に近づいていきます。
この曲線が連続した値に対しての確率をあらわしていることになり、連続的に確率が変化していることから連続分布といわれます。
またこの曲線は確率密度関数と呼ばれ、$f(x)$とあらわします。
連続分布における確率密度関数$f(x)$には以下の性質があります。
$$ すべてのxに対して、0 \leq f(x) \leq 1 $$ $$ \int_{-\infty}^{\infty} f(x)dx = 1 $$
すべての$x$に対して、$ 0 \leq f(x) \leq 1 $というのは連続分布はどの確率変数$x$に対しても必ず確率密度関数は0以上1以下であるということです。
これは、離散分布と同様に確率が0より下回ることもないですし、1より大きくなることもないことを示しております。
$ \int_{-\infty}^{\infty} f(x)dx = 1 $は連続分布のすべての確率変数$x$に対して、確率密度関数を積分すると1となるということです。
これも、離散分布と同様にある事象のすべての確率を合計したら1となるということと同じことを示します。
そして、データ分析におけるもっとも重要な性質は、あるデータの範囲を確率変数としてあつかうことで、データが取り得る確率を積分を用いてあらわすことができます。
その性質は以下の通りです。
$$ 確率Pr\{a \leq x \leq b \} = \int_{a}^{b} f(x)dx $$
まず、$a 〜 b$のデータの値を設定し、そのデータの範囲で確率密度関数$f(x)$を積分することで、$a 〜 b$のデータになる確率を計算することができます。
これを利用することで、データの値の予測をしたり、検定を行うことが可能です。
たとえば、あらかじめデータの確率を5%と95%に設定し、この5%〜95%のデータの範囲になるような確率密度関数を計算することで、そのデータの推定をしたりします。
しかも、確率密度関数の計算はまったく行う必要はなく、具体的にはそれぞれ適応する確率密度関数に対する分布表がありますので、その分布表の値を使って推定していきます。
以上が、連続分布の解説となります。
【統計学で使う確率を理解する】確率分布について:まとめ
いかがでしたでしょうか?以下まとめです。
- 確率変数とは、ある事象に対してどのような確率をとるのか決まっているという性質を持っている変数のことである
- 確率分布とは、確率変数がどのような値になるのか法則性があるもののことである
- 確率分布には、離散分布と連続分布の2つがある
- 離散分布は、確率変数1つ1つに対してそれぞれの確率が存在する確率分布
- 連続分布は、確率変数が連続的な値をとるときにその確率の状態をあらわす確率分布
- 連続分布はデータ分析の分野でよく使用しており、連続分布の確率密度関数を積分することで推定や検定を行うことが可能となる
みなさんも、ぜひ確率分布をマスターして、データ分析をより深く理解していきましょうね!
統計学をもっと勉強したい方へ
確率分布などより深い統計学についてもっと勉強したい方は「入門 統計解析法」の本がおすすめです。
この本では、基本統計量・ヒストグラム・確率分布・正規分布といった基礎的な内容から、実務で使う推定・検定・分散分析・回帰分析までを網羅的に学ぶことができます。
また、実務で使う統計学については、実例を用いながら勉強することができますので、具体的なイメージを持って統計学を勉強することができる一冊となります。
高校数学までの勉強は必要となりますが、それさえ勉強できていれば、統計学全体を理解するのにおすすめの本となります。
統計学の基礎を勉強してみたい、実務での統計学の例を見ながら統計学を学びたい方にとってはぜひ手に取ってみてほしい本となります。
ただ高校数学が難しいと感じる場合は「完全独習 統計学入門」という本で一度勉強してみるのもおすすめです。
こちらの本では、中学までの数学を使いながらなんとなく統計学ってこういう学問だよっていうことを理解するのに適しています。
入門者向けの本ですが、ヒストグラム・基本統計量といった基礎的な内容から実務で使える推定までできるだけ平易な言葉で解説しています。
とてもわかりやすく、難しい公式や専門用語をほとんど使わないため、文系の人でも統計学を学ぶのに適した本です。
統計学ってどういう学問なのか簡単に知りたい方や高校の数学が苦手だけど統計学を勉強したい方にとってはぜひ読んでほしい一冊となります。
みなさんもぜひ統計学について勉強してみてくださいね!
最後までこの記事を読んでいただきありがとうございました!
データサイエンティストになりたい方におすすめの動画講座はこちら
![]()





コメント