こんにちは、かじつとむです。
みなさん、集合とはご存知でしょうか?
「8時だョ!全員集合」という番組があったように、なんとなく集まりをイメージする人が多いと思います。
実は、この集合というのはデータ分析や統計学を勉強する上で必要なことです。
今回はそんな集合について解説します。
この記事を読むことで以下のことがわかります。
- 集合とはどういうものなのかを理解することができる
- 集合の表し方について理解できる
- 集合をなぜ勉強するのかを理解できる
それでは、いってみましょう!
データ分析に必要な集合:集合とは?
集合とは、何かしらの定義によって仲間であるかどうかを判断するものです。
たとえば、理系科目であったり、1〜10までの数字といったものを集合といいます。
集合に含まれている1つ1つをその集合の要素といいます。
たとえば、1〜10までの数字の集合に対して、$1, 1.1, \dfrac{3}{2}, 9.99$はすべて集合の要素となります。
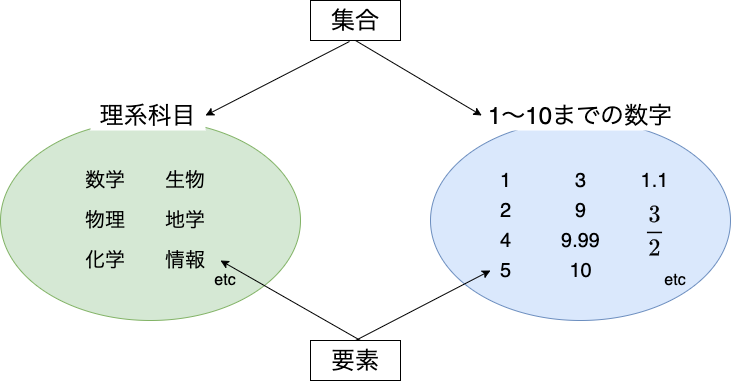
一般的に、要素は小文字のアルファベット($a, b, x$)を、集合は大文字のアルファベット($A, B, P$)を使って表します。
また、ある$x$が集合$A$に属している場合は、$x \in A$と表し、属していない場合は$x \notin A$と表します。
集合や要素がわかったところで、次は集合の表し方について説明します。
データ分析に必要な集合:集合の表し方
集合の表し方は2種類あります。それぞれ以下の通りです。
- 中括弧{}の中に、要素を並べて入れる
- 中括弧{}の中に、要素の代表を好きな文字(一般的には$n$や$x$)で表し、縦棒(|)をはさんで、右側に要素の条件を書く
どちらも中括弧{}を使って集合を表します。
たとえば、1〜10の整数の集合$A$を表す場合、以下の方法で表します。
$$ \begin{eqnarray}
A = \{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 \} \\
A = \{ x|1 \leq x \leq 10, xは整数 \}
\end{eqnarray}$$
このように同じ集合でも表し方2つあるということを覚えておいてください。
集合の表し方がわかったところで、次は集合がなぜ必要であるかを考えていきましょう!
データ分析に必要な集合:集合が必要である理由
集合が必要である理由は、データ分析をする際に、データをわけるのに使われます。
たとえば、20代の身長のデータをヒストグラムで表すとします。
すると以下のようなヒストグラムが作成されます。
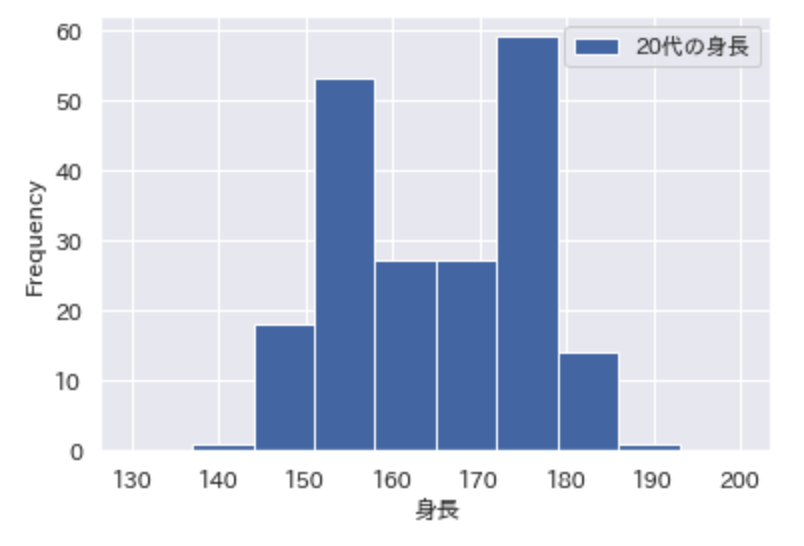
このヒストグラムは、2つの山になっていることがわかります。
つまり2つの性質が異なるデータが混在している可能性があります。
そこで、2つの性質を男性と女性という集合にわけて、再度ヒストグラムを作成すると、以下のようになります。
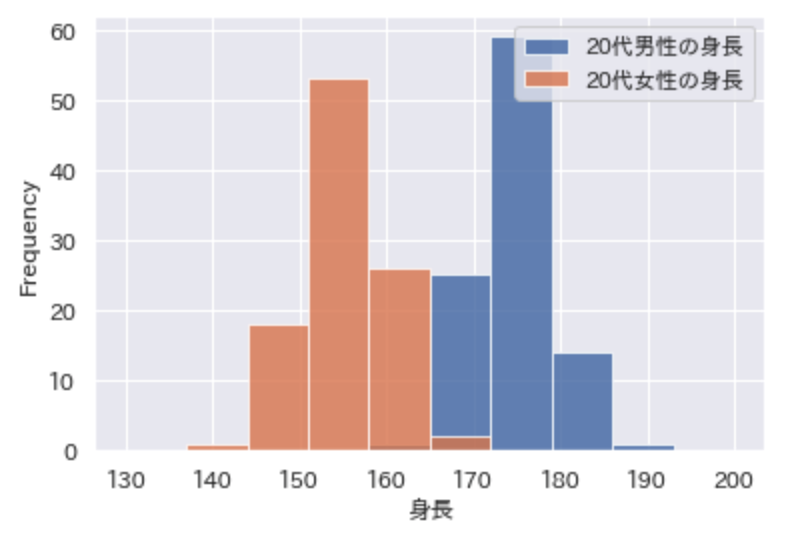
男性と女性にわけて分析を行なった結果、それぞれのヒストグラムが正規分布になっていることがわかります。
つまり、男性と女性という2つの集合にわけてデータを分析することで、データの特徴を掴むことができたということになります。
このように、集合を使うことでデータをわけることで、データの特徴を掴みやすくできます。
データ分析に必要な集合:まとめ
いかがでしたでしょうか?以下まとめです。
- 集合とは、何かしらの定義によって仲間であるかどうかを判断するもの
- 集合の表し方は2種類あり、中括弧{}を用いて要素すべてを並べたり、中括弧{}を用いて代表の文字を使って集合の条件を書く方法がある
- 集合はデータをわける手段として使われ、データの特徴を掴みやすくすることができる
みなさんも集合の考え方を使いながら、ぜひデータ分析に役立ててみてくださいね!
データ分析に必要な集合:最後に
先ほど紹介した集合や確率を勉強するのにおすすめの書籍を紹介します。
統計学に興味を持ち、その基礎となる集合や確率について勉強したい方はぜひおすすめの書籍となります。
集合や確率を勉強するのにおすすめの書籍
ふたたびの確率・統計 [1] 確率編は、統計学に必要な集合や場合の数、確率について理解するのにおすすめの書籍となります。
まず、集合の基礎についてわかりやすく、かつ、数学的な記号についても網羅的に学ぶことができます。
その後で場合の数、とくに場合の数の計算で使われる順列や組合せについてひと通り理解できる内容になっております。
後半では、いよいよ確率を考えるための定義であったり、実際の確率の計算方法について基礎問題から大学入試レベルの問題を使って解説しています。
最後には、大学入試問題を使った腕試しもできるので、高校生にとってもおすすめの書籍となります。
数学の用語等も図解でわかりやすく、かつ丁寧に解説しておりますので、中学や高校生のときに数学が苦手だった方でもとっつきやすい本となります。
もしこの本で勉強したい方がいれば、ぜひ以下のリンクからどうぞ!
ぜひ、統計学やデータ分析の勉強に活かしてみてくださいね!
最後までこの記事を読んでいただきありがとうございました!




コメント