こんにちは、かじつとむです。
突然ですがみなさん、10進法と2進法についてはご存知でしょうか?
この10進法と2進法は人間がコンピュータを指示するのにとても重要な数学の概念となります。
今回はそんな10進法と2進法について説明します。
この記事を読むことで以下のことがわかります。
- 10進法と2進法の概念について理解することができる
- 10進法と2進法の数え方と変換方法ついて理解できる
- 2進法の使われ方が理解できる
それではいってみましょう!
10進法と2進法:10進法とは
10進法は普段私たちが日常生活で使っている数字で、以下の特徴があります。
- 数字の種類は、0, 1, 2, 3, 4, 5, 6, 7, 8, 9の10種類
- 数字の桁には意味があり、右から1の位、10の位、100の位、1000の位・・・をあらわす
たとえば、1908を10進法で考えてみましょう。
まず1908は1, 9, 0, 8の4つの数字を左から並べています。
1は1000の位の数、9は100の位の数、0は10の位の数、8は1の位の数となり、以下のようにあらわします。
$$ 1908 = 1 \times 1000 + 9 \times 100 + 0 \times 10 + 8 \times 1$$
このとき1, 10, 100, 1000は10の何乗といった表現をすることができるため、以下のようにあらわします。
$$ 1908 = 1 \times 10^3 + 9 \times 10^2 + 0 \times 10^1 + 8 \times 10^0 $$
10進法のnの位は$10^n$という表現をします。
この10を10進法の基数または底といいます。また、10の何乗(10の右肩に乗っている数)を指数と言います。
10進法と2進法:2進法とは
2進法はコンピュータで使う数字で、以下の特徴がわかります。
- 数字の種類は0, 1の2種類
- 右から1の位、2の位、4の位、8の位・・・をあらわす
2進数を順番で数えると、以下のようになります。
$$ 0 \rightarrow 1 \rightarrow 10 \rightarrow 11 \rightarrow 100 \rightarrow 101 \rightarrow \cdots $$
1の次は桁が変わり10とあらわし、11の次も桁数が変わり100といったようにあらわしていきます。
具体例として、1010を2進法で考えてみましょう!
この場合、最初の1は8の位の数、次の0は4の位の数、次の1は2の位の数、最後の0は1の位の数となり、以下のようにあらわします。
$$ 1010 = 1 \times 8 + 0 \times 4 + 1 \times 2 + 0 \times 1 $$
このとき1, 2, 4, 8は2の何乗といった表現をすることができるため、以下のようにあらわします。
$$ 1010 = 1 \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + 0 \times 2^0 $$
2進法のnの位は$2^n$という表現をします。
この2は2進法の基数または底となります。
10進法と2進法:2進法から10進法に変換する方法
2進法から10進法に変換する場合は、2進法のそれぞれの位の値と数字を掛けて、その合計をすることであらわすことができます。
たとえば先ほどの2進数の1010を10進法であらわすと以下のようになります。
$$ \begin{eqnarray} 1010(2進法)= 1 \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + 0 \times 2^0 \\ = 1 \times 8 + 0 \times 4 + 1 \times 2 + 0 \times 1 \\ = 8 + 0 + 2 + 0 \\ = 10(10進法) \end{eqnarray} $$
このように2進法の桁数と数字を掛けて、それらを足し合わせることで10進法に変換することができます。
10進法と2進法:10進法から2進法に変換する方法
10進法から2進法に変換する場合は基数変換をします。
10進法から2進法の基数変換の場合、数字を2で割っていき、あまりが0か1かどうかを確認し、0になるまで割り続けます。
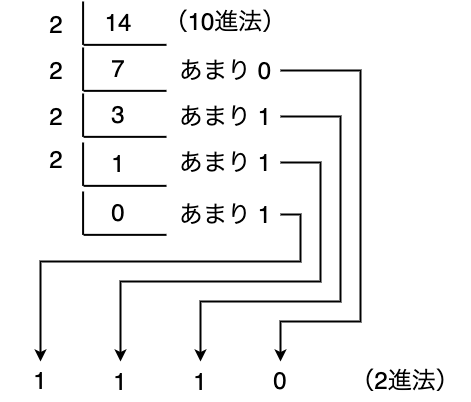
0まで割り切った後に、0からのあまりを左から順番に並べることで10進法から2進法に変換することができます。
10進法と2進法:2進法がコンピュータで使われる理由
2進法がコンピュータで使われている理由は、コンピュータのスイッチが切れている状態と入っている状態をかんたんにあらわすことができるからです。一般的にコンピュータの2進法は以下の通りにあらわすことができます。
- 0:スイッチが切れている状態
- 1:スイッチが入っている状態
このスイッチをたくさん並べることで複雑な仕組みをつくりだすことができます。一方で桁数が大きくなるため、人間にはわかりづらい表記になってしまいます。
人間は、指が10本あることと桁数が少なく数値を表現できるため10進法を直感できます。しかし、コンピュータにとっては、数の種類が多いことによって計算をより複雑になるという欠点があります。
最後に人間がコンピュータを使って計算する場合を考えてみましょう!
人間がコンピュータを使って計算する場合は、10進法の数値をコンピュータに入力し、一度2進法に変換してから計算して、再度10進法に変換して表示されます。
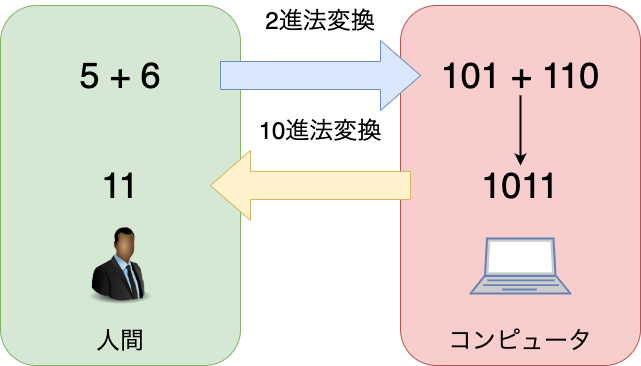
たとえば「5+6」を計算する場合、5と6を2進法で「101」と「110」に変換してから計算し、その結果の「1011」を10進法に変換して、11を最終結果として表現します。
【コンピュータの数学を考える】10進法と2進法:まとめ
いかがでしたでしょうか?以下まとめです。
- 10進法は普段私たちが日常生活で使っている数字で、10種類の数字を使って、右から1の位、10の位、100の位、1000の位・・・といった数値の表現をする
- 2進法はコンピュータで使っている数字で、0と1の2種類の数字を使って、右から1の位、2の位、4の位、8の位・・・といった数値の表現をする
- 2進法から10進法に変換する場合は、2進法のそれぞれの位の値と数字を掛けて、その合計をすることであらわすことができる
- 10進法から2進法に変換する場合は基数変換をする
- 2進法がコンピュータで使われている理由は、コンピュータのスイッチが切れている状態と入っている状態をかんたんにあらわすことができるためである
みなさんも2進砲と10進法を理解しながら、ぜひコンピュータで使う数字について興味を持っていただけたら幸いです!
コンピュータで使う数学をもっと勉強したい方へ
コンピュータで使う数学をもっと勉強する場合は、「プログラマの数学」がおすすめです。
この本では、プログラマになるために必要な最低限の数学の内容を網羅的に解説しています。
先ほどの、2進法と10進法の話はもちろん、論理や剰余、帰納法、順列・組合せ、再帰や指数といった数学の内容を勉強することができます。
後半では、問題の解き方や機械学習の第一歩といったプログラマの考え方を解説している本となっています。
図解でわかりやすいこともさることながら、クイズ形式で実際に解いてみることもできる本となっています。
プログラマーになりたい人で、基礎的な数学を理解したい方にはぜひおすすめの1冊となっていますので、もしよろしければ以下のリンクからどうぞ!
みなさんも、この本を読んでぜひコンピュータサイエンスやプログラマーが使っている数学を理解してみてください!
最後までこの記事を読んでいただきありがとうございました!




コメント