こんにちは、かじつとむです。
前回、集合の概要や集合の種類について解説しました。
今回は、集合に関する法則、ド・モルガンの法則について解説します。
この記事を読むことで以下のことがわかります。
- 集合の法則であるド・モルガンの法則について理解できる
- ド・モルガンの法則を通して集合やデータを分類する上での重要な考え方について理解できる
それではいってみましょう!
集合の法則 ド・モルガンの法則とは
ド・モルガンの法則は集合A、Bに対して和集合や共通部分の補集合に以下の関係が成り立つことをいいます。
$$ \overline{(A \cup B)} = \overline{A} \cap \overline{B} $$ $$ \overline{(A \cap B)} = \overline{A} \cup \overline{B} $$
まずは、$ \overline{(A \cup B)} = \overline{A} \cap \overline{B} $について解説します。
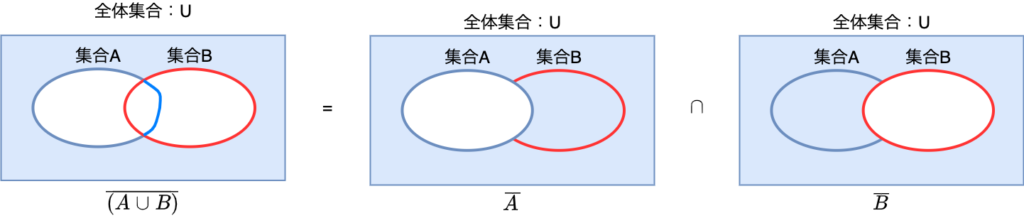
上の図では、青色のハッチングしている部分が集合の要素となり、ハッチングしていない部分は要素ではないことをあらわします。
Aの補集合となる部分とBの補集合の共通部分を抜き出すと、上の図のようにAとBの和集合ではない部分、すなわち$A \cup B$の補集合となります。
次に、$ \overline{(A \cap B)} = \overline{A} \cup \overline{B} $について解説します。
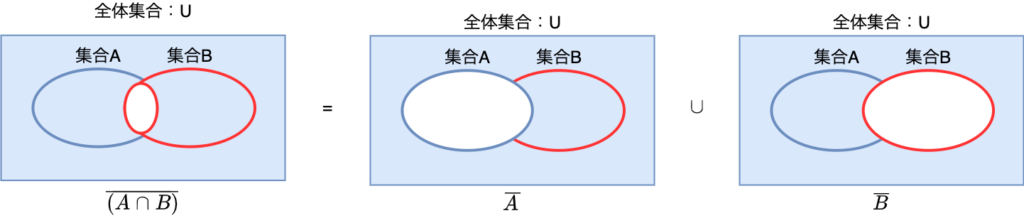
Aの補集合となる部分とBの補集合の和集合を抜き出すと、上の図のようにAとBの共通部分ではない部分、すなわち$A \cap B$の補集合となります。
ここで重要なのは、「かつ」の否定は「または」となり、「または」の否定は「かつ」となることです。
$$ \overline{(p かつ q)} = \overline{p}または\overline{q} $$ $$ \overline{(p または q)} = \overline{p}かつ\overline{q} $$
たとえば、「年収1千万以上」かつ「既婚者」の否定は「年収1千万未満」または「未婚者」となります。
「焼肉が好き」または「寿司が好き」の否定は「焼肉が嫌い」かつ「寿司が嫌い」となります。
このように「かつ」に否定は「または」、「または」の否定は「かつ」となることは、集合を考えたり、データを分類する上ではとても重要な考えとなります。
集合の法則:ド・モルガンの法則のまとめ
いかがでしたでしょうか?以下まとめです。
- ド・モルガンの法則とは、「2つの集合の補集合の共通部分を抜き出すと、2つの集合の和集合の補集合」となったり、「2つの集合の補集合の和集合を抜き出すと、2つの集合の共通部分の補集合」となる法則
- すなわち「かつ」の否定は「または」となり、「または」の否定は「かつ」となることあらわす法則
みなさんもぜひ集合の法則を理解して、データの分類方法について考えてみてください!
集合や確率についてもっと勉強したい方へ
先ほど紹介したド・モルガンの法則や確率についてもっと勉強したい方は、「ふたたびの確率・統計[1]確率編」がおすすめです。
この本では、集合・確率や数学的に使われている記号についても網羅的に学ぶことができます。
特に、集合や確率については高校数学の基礎レベルから大学入試レベルまで、より実践的な問題を使って解説しております。
最後は、力試しとして大学入試問題を使った練習問題もありますので、高校数学の参考書としてもおすすめの本となります。
集合や確率について、図解で直感的にも理解できる本となっておりますので、文系の方や数学をもう一度基礎から学びたい方は、ぜひ以下のリンクからどうぞ!
みなさんもぜひ集合や確率について勉強してみてくださいね!
最後までこの記事を読んでいただきありがとうございました!







コメント