こんにちは、かじつとむです。
前回、集合の概要について解説しました。
今回は、実際にどのような集合があるのかをまとめてみました。
この記事を読むことで以下のことがわかります。
- 集合にはどのようなものがあるのか理解することができる
- 集合の種類をイメージしやすくなる
それでは、いってみましょう!
集合の種類:結論
覚えておいてほしい集合は以下の通りです。
- 部分集合と空集合
- 共通部分と和集合
- 全体集合と補集合
それぞれの集合について解説します。
集合の種類:部分集合と空集合
2つの集合A, Bについて、Bの要素がすべてAの要素となる場合、BはAに含まれるといいます。
このように、BはAに含まれる集合のことをBはAの部分集合といいます。
BはAの部分集合であることを記号であらわすと以下の通りになります。
$$ BはAの部分集合:B \subset A または A \supset B $$
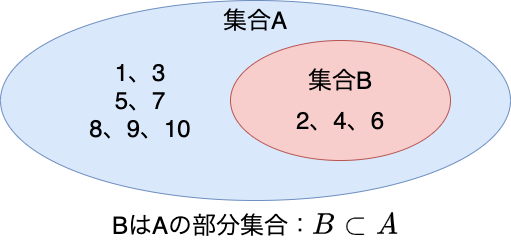
たとえば、Aは1〜10の整数の集合であり、Bは2, 4, 6の要素からなる集合であるとします。
この場合、Bの要素はすべてAに含まれますので、BはAの部分集合であるといえます。
このような集合の状態を図であらわすと以下のようになります。
また、集合Aの要素と集合Bの要素が完全に一致する場合、AとBは等しいといいます。
この場合、記号では以下の通りにあらわします。
$$ 集合AとBが完全一致:A = B $$
要素を持たない集合を空集合といいます。空集合は記号で以下のようにあらわします。
$$ 空集合:\varnothing $$
空集合は要素を持たないため、どんな集合に対しても部分集合となります。
以上が部分集合と空集合の解説でした。
集合の種類:共通部分と和集合
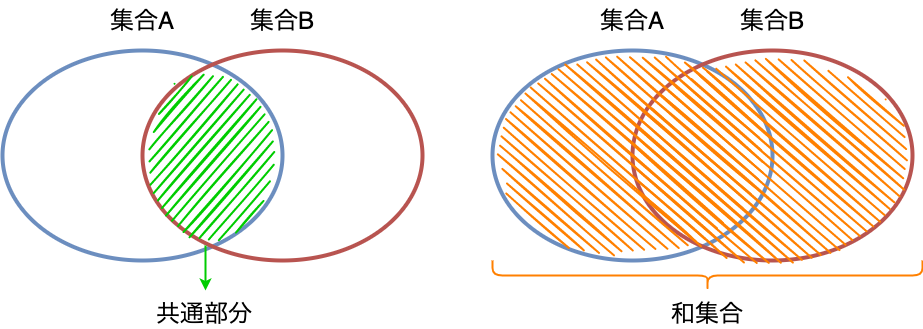
2つの集合A, Bに対して、どちらにも属する要素すべての集合を共通部分といいます。
AとBの共通部分は記号で以下のようにあらわします。
$$ 集合AとBの共通部分:A \cap B $$
記号である「$\cap$」は、日本語では「かつ」、英語では「cap」と呼びます。
また、AとBの共通部分は要素$x$を使って以下のようにあらわすこともできます。
$$ 共通部分:A \cap B = \{ x \mid x \in A かつ x \in B \} $$
2つの集合A, Bに対して、少なくともどちらか一方に属する要素すべての集合を和集合といいます。
AとBの和集合は記号で以下のようにあらわします。
$$ 集合AとBの和集合:A \cup B $$
記号である「$\cup$」は、日本語では「または」、英語では「cup」と呼びます。
また、AとBの和集合は要素$x$を使って以下のようにあらわすこともできます。
$$ 和集合:A \cup B = \{ x \mid x \in A または x \in B \} $$
集合Aと集合Bの共通部分と和集合を図であらわすと以下のようになります。
共通部分と和集合の例は次のようなものがあります。
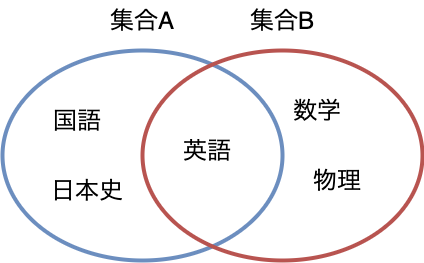
ある大学入試の文系の学科を受けるときに必要な科目の集合をA ={国語、日本史、英語}とします。
一方、理系の学科を受けるときに必要な科目の集合をB = {数学、英語、物理}とします。
このとき、大学入試として共通して受けなければいけない科目の集合を以下のようにあらわします。
$$ 共通の科目の集合:A \cap B = \{ 英語 \} $$
また、文系・理系どちらの学科も受けたい場合、その科目の集合を以下のようにあらわします。
$$ 文系・理系の科目の集合:A \cup B = \{ 国語、日本史、英語、数学、物理 \} $$
以上が、共通部分と和集合の解説でした。
集合の種類:全体集合と補集合
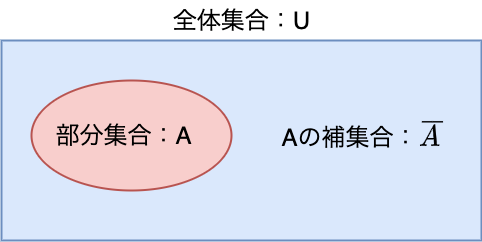
与えられた集合Uに対して、複数の部分集合を考えるとき、その複数の部分集合から見た集合Uを全体集合といいます。
また、全体集合Uに対して部分集合Aを考えるとき、部分集合A以外の集合をAの補集合といいます。
Aの補集合は以下のようにあらわします。
$$ Aの補集合:\overline{A} または A^c $$
また、補集合$ \overline{A} $を要素$x$と全体集合Uを用いて次のようにあらわせます。
$$ Aの補集合:\overline{A}=\{ x | x \in U かつ x \notin A \} $$
以上より、全体集合Uと部分集合A、Aの補集合$\overline{A}$を図であらわすと以下のようになります。
また、全体集合Uと空集合$ \varnothing $はUの部分集合:AとAの補集合$ \overline{A} $を用いて、以下の関係であることをあらわします。
$$ A \cup \overline{A} = U, A \cap \overline{A} = \varnothing $$
以上が全体集合と補集合の解説でした。
集合の種類:まとめ
いかがでしたでしょうか?以下まとめです。
- 2つの集合A, Bについて、Bの要素がすべてAの要素となる場合、BはAの部分集合である
- 要素を持たない集合を空集合という
- 2つの集合A, Bがあるとき、どちらの要素にも含まれる集合を集合A, Bの共通部分という
- 2つの集合A, Bがあるとき、どちらか一方に含まれている集合をA, Bの和集合という
- 全体集合Uに対して、部分集合をAとするとき、部分集合A以外の集合をAの補集合という
みなさんも、集合の種類を覚えてみてくださいね!
集合や確率についてもっと勉強したい方へ
先ほど紹介した集合や確率についてもっと勉強したい方は、「ふたたびの確率・統計 [1] 確率編」がおすすめです。
この本では、集合や確率や数学的に使われる記号についても網羅的に勉強することができます。
特に、確率については基礎から大学入試レベルまでより実践的な問題を使って解説しております。
最後は、大学入試問題を使った練習問題もありますので、高校生にとってもおすすめの本となります。
集合や確率について、図解でわかりやすく、かつ丁寧に解説しておりますので、文系の方や数学が苦手だった方がもう一度勉強するにはとてもとっつきやすい本です。
もしこの本で勉強した方がいれば、ぜひ以下のリンクからどうぞ!
みなさんもぜひ集合や確率について勉強してみてくださいね!
最後までこの記事を読んでいただきありがとうございました!





コメント