こんにちは、かじつとむです。
前回、基本統計量について特に平均値・分散・標準偏差についての意味や求め方について解説しました。
しかし、平均値や分散、標準偏差でどうやってデータを解析すれば良いのかわからない人もいると思います。
そこで、今回は平均値や分散・標準偏差を使ったデータ解析の方法について解説します。
この記事を読むことで以下のことがわかります。
- 平均値、分散、標準偏差の基本的な使い方がわかる
- 基本的なデータ解析方法を身につけることができる
それではいってみましょう。
平均値・分散・標準偏差からデータ解析方法:平均値・分散・標準偏差とは
平均値とはデータの合計をデータの数で割ることで得られる値です。
平均値はデータの中心的な値であり、データの範囲内にあります。
分散とはデータのばらつき具合を評価できる指標です。
具体的にはすべてのデータと平均値の差の2乗を取り、その合計をデータの数で割った値となります。
標準偏差は、分散の平方根をとった値です。
標準偏差にすることで、平均値やデータそのものと比較ができるようになります。
平均値・分散・標準偏差についてもっと知りたい方は以下の記事をご参照ください。
平均値・分散・標準偏差を使ったデータ解析方法:正規分布とは
正規分布とは以下の図のようにデータのヒストグラムをとったとき、山が1つで左右対称の形状を持つものをいいます。
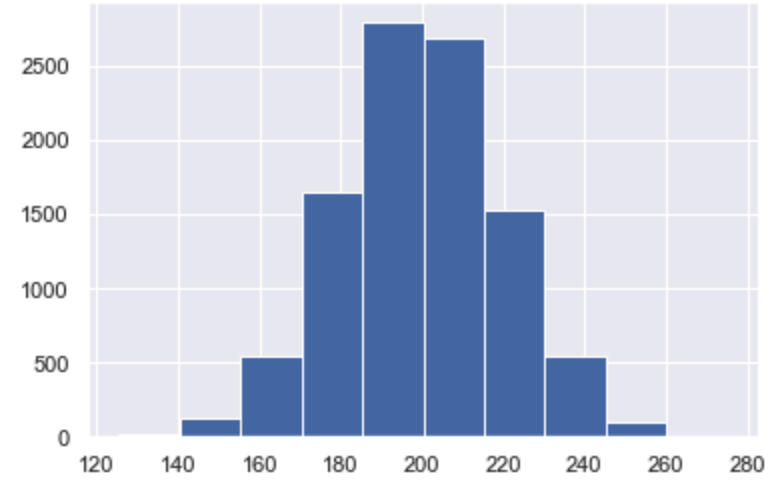
正規分布であることは平均値がデータの中央に存在し、かつ均等にデータがばらつくことを示します。
また、新しいデータが入ったとしても平均値に近い値になる可能性が高く、平均値より離れた値にはなりにくいのも正規分布の特徴です。
正規分布やヒストグラムについてもっとよく知りたい方は以下の記事をご参照ください。
平均値・分散・標準偏差を使ったデータ解析方法 その1:確率密度関数を用いて解析する
それでは、平均値と標準偏差からデータが普通か特殊かの判断方法を説明します。
まず、大前提としてデータの分布が正規分布であることが必要です。
なぜなら、データが正規分布に従うことでデータの平均値である確率がもっとも高く、離れていく大きさによって、そのデータの確率も同じだけ低くなるからです。
以下の図では、平均値が200で標準偏差が20のときの正規分布のデータを示します。
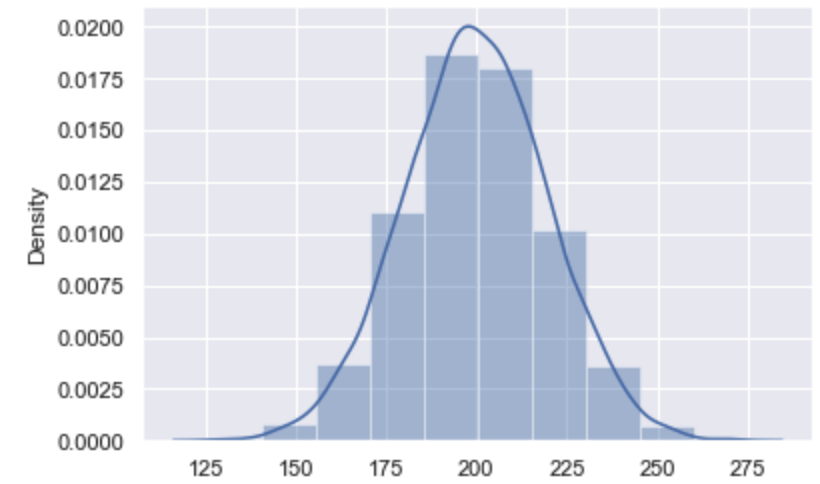
この場合ですと、平均値200に近いデータである可能性が高く、そこから離れていくほどそのデータの可能性は低いことを示しています。
また、この図における曲線を正規分布の確率密度関数といいます。
確率密度関数とは文字通り確率を計算するための関数のこといいます。
正規分布の確率密度関数は次のような式で表します。
$$ f(データの値) = \frac{1}{\sqrt{2\pi \times 分散}} \times \exp (-\frac{(データの値 – 平均値)^2}{2 \times 分散}) $$
少し難しいかもしれませんが、重要なのはデータの値と平均値と分散がわかっていれば、データの値に対する確率がわかるということです。
すなわち、データに対する確率が大きければ大きいほどそのデータは普通であり、逆に小さければ小さいほどそのデータは異常であることがわかります。
しかし、「確率密度関数が少しわかりにくい」「そもそも計算することがめんどくさい」と思ったかもしれません。
でもご安心ください。次は標準偏差を使ったもっと簡単な方法をご紹介します。
平均値・分散・標準偏差を使ったデータ解析方法 その2:標準偏差を使ったデータの解析方法
標準偏差を使った方法は、データが平均値に対して標準偏差の何個分離れているのかでデータを解析します。
以下の図では、平均値200で標準偏差20の正規分布のデータはどのように解析できるのかを示します。
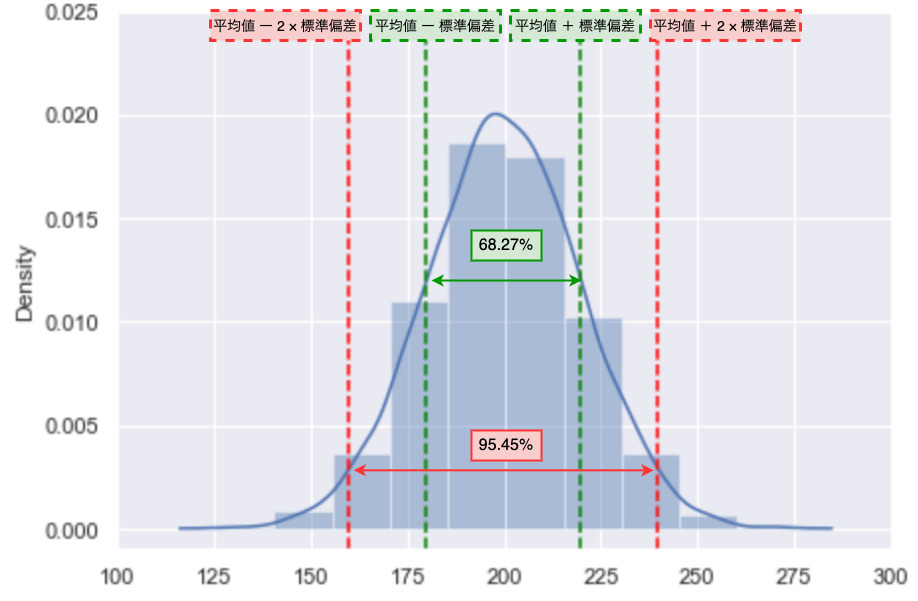
データが正規分布である場合、平均値に対して標準偏差が±1個分の範囲であれば68.27%の確率でそのデータ範囲に収まることを示しています。
また、平均値に対して標準偏差が±2個分の範囲であれば95.45%の確率でそのデータ範囲収まることを示しています。
このように、データが正規分布であれば、データが平均値に対して標準偏差が何個分離れているのかという指標でデータの評価が可能であることがわかります。
一般的には、平均値から標準偏差の±2個分まで範囲の離れ方であれば、データは普通とみなし、それ以上離れていればデータは異常であるもしくは特殊であると解析できます。
平均値・分散・標準偏差を使ったデータ解析方法:3σ・4σとは
最後に、製造業で使われる3σ・4σについて説明します。
3σ・4σとは平均値に対して標準偏差が±3個分、4個分のデータの範囲のことを指します。
では、なぜ3σ・4σが製造業で使われているのでしょうか?
答えは製造業における工場の優劣は3σおよび4σの範囲の中で品質が保持できるかどうかが重要だからです。
下の表にて標準偏差と保証できる品質の割合について示します。
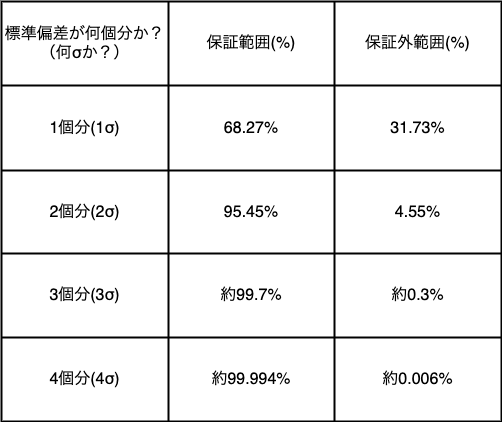
3σのとき、保証範囲は99.7%と大きく異常である可能性は0.3%と小さいため、工場において十分な能力を持っているということが数値としてわかります。
もっと優秀な能力が必要である場合には4σを使用します。
これは保証範囲は99.994%とほとんどすべてのものに対して保証できるということを示しており、同時に異常である可能性は0.006%とほんのごくわずかの可能性以外は異常は発生しないことを示します。
余談ですが、3σのことを保証外範囲0.3%から精密な品質(1,000分の3で以上が発生することより)といい、4σのことを保証外範囲0.006%から万が一の品質(10,000分の1よりも小さい可能性で発生することより)ということもあります。
平均値・分散・標準偏差を使ったデータ解析方法:まとめ
いかがでしたでしょうか?最後にまとめます。
- データが正規分布であるとき、平均値・分散・標準偏差を用いてデータを解析できる
- 平均値・分散を使って確率密度関数からデータの発生確率を計算してデータを解析できる
- 平均値に対して標準偏差が何個分離れているのかによってデータが普通か異常かを判別できる
みなさんも、この記事を読んでぜひデータの解析をやってみてください!
統計学を使ったデータ解析方法を学びたい方へ
統計学を使ってもっとデータの解析方法を学びたい方は、「入門 統計解析法」がおすすめです。
この本では、平均値・分散・標準偏差を使った基本的なデータ解析方法から仮説検定・分散分析・回帰分析といった製造業の現場で実践的に使える統計学について学ぶことができます。
高校数学の数式を使いますが、実際の製造業で使われる具体例を用いて統計学を解説しておりますので、データ解析方法をイメージできる一冊となります。
数学の知識を持っており、実務で使える本格的な統計学やデータ解析方法について学びたい方にはおすすめの1冊です。
ただしこちらの本を手に取ってみて、難しいと感じた方は「完全独習 統計学入門」や「〈図解〉基本からよくわかる品質管理と品質改善のしくみ
」がおすすめです。
みなさんも統計学をビジネスや製造現場で使えるようになりましょう!
最後までこの記事を読んでいただきありがとうございました!
新しい学びを探したい方はこちら!
![]()








コメント