こんにちは、かじつとむです。
今までの仮説検定では1つの母集団について検証する方法を解説してきました。
今回は2つの母集団の平均値に差があるのかを検定する方法について解説します。
第1弾として母分散がわかっている場合、もしくは標本の数が大きい場合の検定方法について解説します。
この記事を読むことで以下のことがわかります。
- 母分散が既知である、または標本の数が大きい場合の2つの母平均の差の検定方法について理解できる
- 1つの母集団で行う場合の検定との違いについて理解できる
それではいってみましょう!
2つの母平均の差の検定(母分散が既知):結論
母分散が既知の場合のあ2つの母平均の差の検定方法は以下の手順で行います。
- 帰無仮説と対立仮説を設定する
- 有意水準を決める
- 母集団の情報から使用する確率分布と棄却域を決める
- 得られたデータから検定統計量を計算する⇦ここが違う!!
- 検定統計量と棄却域を比較し、帰無仮説を棄却するかどうか判断する
基本的には1つの母集団を検証する仮説検定の方法と同じです。
1つの母集団に関する仮説検定の詳細を知りたい方は以下のリンクからどうぞ!
しかし、1つだけ通常の仮説検定とは違うところがあります。
それが検定統計量の考え方です。次は検定統計量の違いについて解説します。
2つの母平均の差の検定(母分散が既知):検定統計量

検定統計量とは、検定するために使用される値のことをいい、統計量とも呼ばれます。
検定統計量を利用することで、さまざまな確率分布を使って検定することができます。
今回は母分散が既知なので、検定統計量は$z$を使用します。
検定統計量$z$は平均が0、分散が1となるように標本データを標準化した値です。
この統計量は標準正規分布を使って検定することができます。
1つの母集団$N(\mu, \sigma^2)$(母平均:$\mu$, 母分散:$\sigma^2$)のときの検定統計量$z$を考えてみましょう。
この母集団の標本平均を$\bar{x}$、標本データの数を$n$とすると、以下のように検定統計量$z$を計算することができます。
$$ 検定統計量:z = \frac{\bar{x} – \mu}{\sqrt{\frac{\sigma^2}{n}}} $$
この計算の分子は標本平均から母平均を引いた値を示します。
また、分母は標本から得られる推定量のばらつきであり、母分散$\sigma^2$を標本データの数$n$で割った値の平方根であらわします。
この値を標準誤差といいます。
すなわち、検定統計量$z$は標本平均から母平均を引いた値を推定量のばらつきで割った値であることがわかります。
では、2つの母平均の差の検定統計量$z$はどうなるでしょうか?
2つの母集団$N_{1}(\mu_{1}, \sigma_{1}^2)$、$N_{2}(\mu_{1}, \sigma_{2}^2)$とし、それぞれの標本平均を$\bar{x_{1}}, \bar{x_{2}}$、標本のデータの数を$n_{1}, n_{2}$とすると以下のように計算できます。
$$ \begin{eqnarray}
検定統計量:z &=& \frac{(\bar{x_{1}} – \mu_{1}) – \bar{x_{2}} – \mu_{2}}{\sqrt{\frac{\sigma_{1}^2}{n_{1}} + \frac{\sigma_{2}^2}{n_{2}}}} \\
&=& \frac{(\bar{x_{1}} – \bar{x_{2}}) – (\mu_{1} – \mu_{2})}{\sqrt{\frac{\sigma_{1}^2}{n_{1}} + \frac{\sigma_{2}^2}{n_{2}}}}
\end{eqnarray}$$
2つの母平均の差の場合、分子はそれぞれ2つの標本平均と母平均の差同士を引いた値となります。
また分母はそれぞれの母分散を標本データの数で割り、それらの和の平方根となります。
このように2つの母平均の差の検定統計量$z$を計算することができます。
以上が2つの母平均の差の検定統計量となります。
次は具体例を使って2つの母平均の差の検定方法について説明します。
2つの母平均の差の検定方法(母分散が既知):具体例

2つの母平均の差の具体例として以下の問題を考えます。
ある自動車部品の硬さ測定をA工場とB工場で行った。
A工場とB工場でそれぞれ50個測定し、それぞれの平均値が220HV、205HVであった。
この2工場での母分散が25と144であったとき、2工場の硬さの平均値の差はあるか

この具体例を使って実際に2つの母平均の差の検定を行います。
2つの母平均の差の検定方法(母分散が既知)その1:帰無仮説と対立仮説を設定する

まず、帰無仮説と対立仮説を設定します。
今回は2つの工場での自動車部品の硬さの平均値に差があると考えていますので、帰無仮説と対立仮説は以下のように設定します。
- 帰無仮説:2つの工場での硬さの平均値に差がある($\mu_{A工場} = \mu_{B工場}$)
- 対立仮説:2つの工場での硬さの平均値に差がない($\mu_{A工場} \neq \mu_{B工場}$)
2つの母平均の差の検定方法(母分散が既知)その2:有意水準を決める
帰無仮説と対立仮説を設定したら、有意水準を決めます。
有意水準は一般的に5%か1%に設定します。
今回は有意水準を5%に設定します。
2つの母平均の差の検定方法(母分散が既知)その3:母集団の情報から使用する確率分布と棄却域を決める
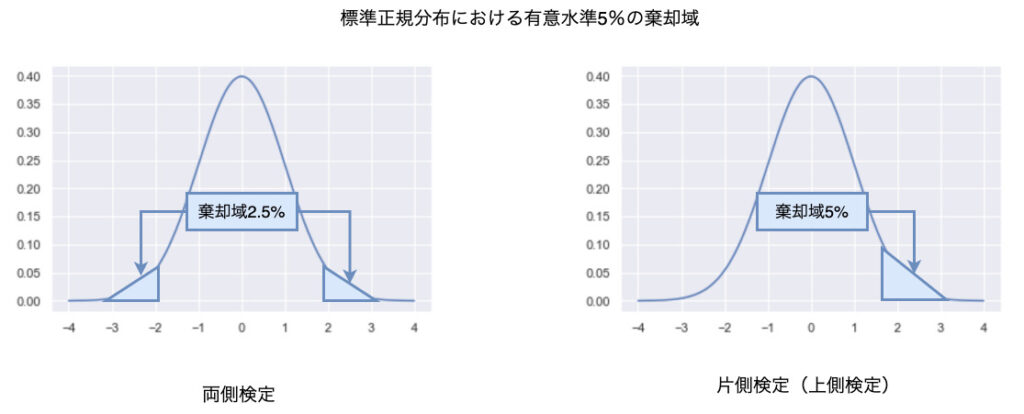
有意水準が決まったら、母集団の情報から使用する確率分布を決めます。
今回は母分散がわかっているので、確率分布は標準正規分布を使用します。
有意水準と確率分布が決まったので棄却域を決めることができます。
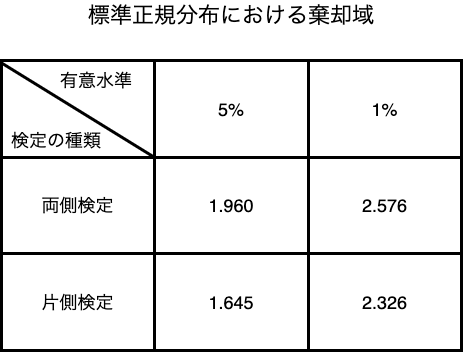
確率分布は標準正規分布なので、標準正規分布表を使って棄却域を決めます。
また、有意水準は5%であり、対立仮説が「2つの工場の硬さの平均値に差がない」ことから両側検定での棄却域を決めます。
以上より、棄却域は標準正規分布の有意水準5%の両側検定の値:1.960を採用します。
2つの母平均の差の検定方法(母分散が既知)その4:得られたデータから検定統計量を計算する
棄却域が決まったら、得られたデータから検定統計量を計算します。
今回は2つの母平均の差の検定であり、かつ母分散が既知であることから検定統計量$z$を計算します。
$$ 検定統計量:z = \frac{(\bar{x}_{A工場} – \bar{x}_{B工場}) – (\mu_{A工場} – \mu_{B工場})}{\sqrt{\frac{\sigma_{A工場}^2}{n_{A工場}} + \frac{\sigma_{B工場}^2}{n_{B工場}}}} $$
ここで帰無仮説「2つの工場の硬さの平均値に差がない」としているため$\mu_{A工場} = \mu_{B工場}$が成り立ちます。
よって母平均の差の部分を消すことができるので、検定統計量$z$は以下のようになります。
$$ 検定統計量:z = \frac{\bar{x}_{A工場} – \bar{x}_{B工場}}{\sqrt{\frac{\sigma_{A工場}^2}{n_{A工場}} + \frac{\sigma_{B工場}^2}{n_{B工場}}}} $$
ここで、A工場の母分散:36・標本平均:220・標本の数:50、B工場の母分散:64・標本平均:205・標本の数:50であるため、検定統計量$z$は以下のように計算できます。
$$ \begin{eqnarray}
検定統計量:z &=& \frac{220 – 205}{\sqrt{\frac{36}{50} + \frac{64}{50}}} \\
&=& \frac{15}{\sqrt{2}} \\
& \fallingdotseq & 10.607
\end{eqnarray} $$
よって検定統計量$z$は10.607となります。
2つの母平均の差の検定方法(母分散が既知)その5:検定統計量と棄却域を比較し、帰無仮説を棄却するかどうか判断する
検定統計量を計算したら棄却域と比較し、帰無仮説を棄却するかどうか判断します。
検定統計量と棄却域を比較し棄却される条件は以下となります。

よって今回の検定統計量は10.607、棄却域は1.960のため以下の鑑定となります。
$$ (検定統計量の絶対値)10.607 \gt 1.960(棄却域) $$
以上の関係から、帰無仮説が棄却される条件を満たしているため、帰無仮説を棄却できます。
すなわち、今回の「2つの工場の硬さの平均値の差がない」という帰無仮説が棄却され、
「2つの工場の硬さの平均値の差がある」という対立仮説が採択されます。
以上が、2つの母平均の差の検定方法(母分散が既知)となります。
2つの母平均の差の検定(母分散が既知の場合)とは:まとめ
いかがでしたでしょうか?以下まとめです。
- 母分散が既知である場合、2つの母平均の差の検定は1つの母集団の検定方法とほとんど同じである。
- 違う点は検定統計量の計算方法であり、それぞれ2つの標本平均から母平均を引いた値を、それぞれの母分散をデータの数で割った値の和の平方根で割った値となる
みなさんもぜひ2つの平均に対する差の検定にチャレンジしてみてください!
検定・推定などの実践的な統計学を勉強したい方へ

推定や検定、回帰分析、分散分析といった実践的な統計学を学びたい方におすすめなのが「入門 統計解析法」です。
この本では、平均値・分散・標準偏差や確率分布といった統計学の基本的なところから、検定や推定・回帰分析・分散分析といったより実践的な統計学について学ぶことができます。
こちらの本では高校までの数学の知識を使いますが、より丁寧にかつ詳しく統計学を勉強することができます。
また、統計学の例題も工場や品質管理に準じた問題を取り上げているので、製造業の方にもどのように統計学を使って良いのか具体的に理解できる内容にもなっております。
より実践的な統計学を学びたい方や、製造業の現場で統計学を使っていきたい方にはおすすめの本となります。
みなさんもぜひ実践的な統計学の勉強にチャレンジしてみましょう!
最後までこの記事を読んでいただきありがとうございました!
統計学から機械学習、ディープラーニングまでを動画で学びたい方はUdemyの「【世界で37万人が受講】データサイエンティストを目指すあなたへ〜データサイエンス25時間ブートキャンプ〜」がおすすめ!





コメント