こんにちは、かじつとむです。
機械学習がどのようなものなのかについて解説していきました。
今回は機械学習の中身を理解する上で必要な数学について解説します。
この記事を読むことで以下のことがわかります。
- 機械学習を学ぶ上で必要な3つの数学について理解できる
- 3つの数学がどのように機械学習に使われるのか理解できる
それではいってみましょう!
機械学習に必要な数学とは:結論

機械学習を学ぶ上で必要な数学は以下の3つです。
- 微積分
- 線形代数学
- 確率統計
それぞれの概要について解説します。
機械学習に必要な数学 その1:微積分
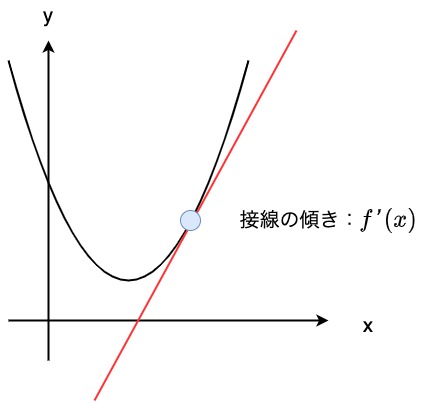
微積分とは、関数に対してある点の接線の傾きを求めたり、ある範囲の面積を計算する手法です。
微積分の特に微分の部分、すなわち関数に対しての接線の傾きを求めることが機械学習にとって重要です。
なぜなら、関数の接線の傾きが0であればその関数の最小値(または最大値)をあらわすことができるからです。
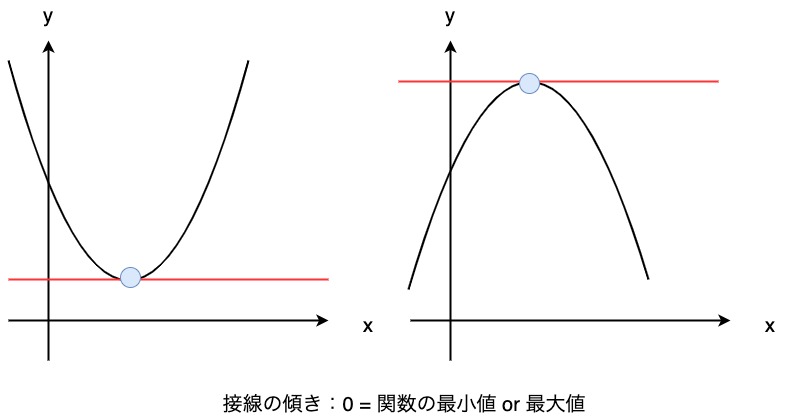
機械学習では、正解データと推定したデータの差の2乗の関数を求めます。
このような差を損失関数といいます。
損失関数がもっとも小さくなる推定用の関数の係数を決めることで、もっとも良い予測をした推定用の関数がつくられます。
このときに損失関数に対して各係数毎の微分をし、その値が0となるところが正解に対して予測できている係数を求めることができます。
またこのようにデータの差の2乗を関数とし、その関数が最小となる係数を決める方法を最小二乗法といいます。
微積分が機械学習にどのように影響するのか、もう少し深く勉強したい方は「【キカガク流】人工知能・機械学習 脱ブラックボックス講座 – 初級編 –」というUdemyの講座がおすすめです。
機械学習に必要な数学 その2:線形代数学

線形代数学とは、かんたんにいうと大量のデータをまとめて計算するための重要な知識です。
たとえば、機械学習の重回帰分析でデータを予測するモデルをつくったとしましょう。
このようなモデルをn個のデータに対して、m個の係数で説明するモデルは通常以下のようにあらわします。
$ \hat{y}_{1} = w_{1}x_{11} + w_{2}x_{12} + \cdots + w_{m}x_{1m} $
$ \hat{y}_{2} = w_{1}x_{21} + w_{2}x_{22} + \cdots + w_{m}x_{2m} $
$ \vdots $
$ \hat{y}_{n} = w_{1}x_{n1} + w_{2}x_{n2} + \cdots + w_{m}x_{nm} $
このようにデータが大きいほど、また係数が多いほどあらわすのが難しいものになります。
しかし、線形代数学を使うことで上記のようなモデルを以下のようにかんたんにあらわすことができます。
$$ モデル:\mathbf{\hat{y}} = X \mathbf{w} $$
この式は$\mathbf{\hat{y}}$がすべてのモデルの予測値のベクトルとしてあらわしております。
そして、右辺では$X$をデータの行列としてまとめ、$\mathbf{w}$を係数をまとめたベクトルとして扱うことで、まとまった式であらわすことができます。
また線形代数学と微積分を組み合わせることで、係数のベクトルである$\mathbf{w}$は以下のようにあらわすことができます。
$$ 係数:\mathbf{w} = (X^{T}X)^(-1)\mathbf{y} $$
ここでの$\mathbf{y}$は正解データとなります。
また、$X^{T}$は転置行列といい、行列$X$の要素をひっくり返した行列のことをいいます。
ここで説明するのは少し難しいのですが、まずは線形代数学と微積分を組み合わせることでモデルの係数をスッキリ計算できるということがわかればOKです。
まとめると以下のようになります。

線形代数学を機械学習に適用する方法や計算など、もう少し深く勉強したい方は「【キカガク流】人工知能・機械学習 脱ブラックボックス講座 – 中級編 –」というUdemyの講座がおすすめです。
機械学習に必要な数学 その3:確率統計
確率統計は、先ほどの微積分や線形代数学よりかはわかりやすい数学だと思います。
なぜなら、統計であれば平均値・分散・標準偏差といった値はビジネスでも生活でも見かけるからです。
また、確率でも「宝くじの当たる確率はどれくらいか?」「天気予報の降水確率」といったように生活に溶け込んでいます。
このような統計学と確率を組み合わせたものが確率統計です。
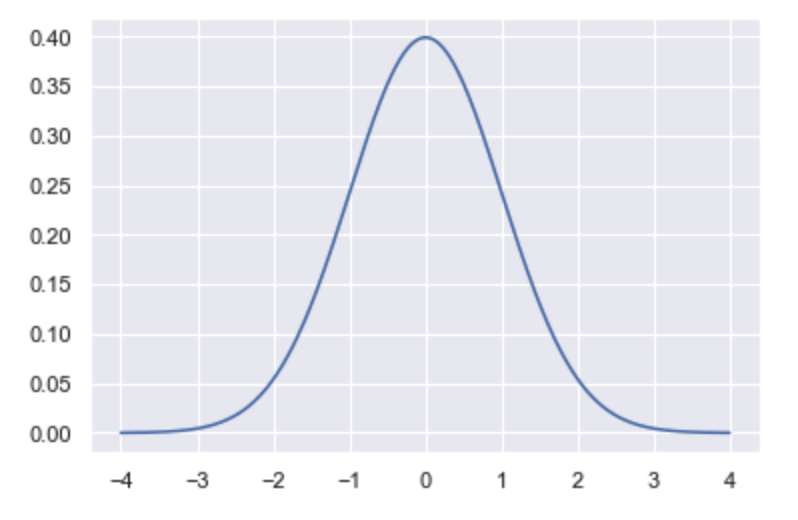
確率統計で重要なのは確率分布です。
データを取得すると必ずばらつきが発生します。
このばらつきが偶然であるものなのか、何かの要素によって起こってしまったものなのかを比較検討するために確率分布を使います。
確率分布についての基礎的な内容についての記事は以下となります。
機械学習では、確率分布を使った比較検討を応用して予測に使っている要素は本当に、予想したい値に関係があるのかどうかを確認するといったような使われ方をします。
確率統計の基礎をしっかり勉強したい方は「【世界で37万人が受講】データサイエンティストを目指すあなたへ〜データサイエンス25時間ブートキャンプ〜」というUdemyの講座がおすすめです。
機械学習に必要な数学とは:まとめ
いかがでしたでしょうか?以下まとめです。
- 機械学習に必要な数学は、微積分、線形代数学、確率統計
- 微積分は特に関数の接線の傾きを求める微分が重要で、これにより最適な関数を求めることができる
- 線形代数学は大量のデータをまとめて計算する方法であり、データの予測値や係数をまとめてあらわすことができる
- 確率統計は確率分布が重要で、これを使うことでデータの予測値に対して要素がどれくらい関係を持っているのかを計算で求めることができる
みなさんも機械学習に挑戦するならば、ぜひこの3つの数学について勉強してみてください!
機械学習の数学基礎を学ぶためのおすすめの本

機械学習の数学を学ぶおすすめの本は「人工知能プログラミングのための数学がわかる本」です。
この本では、機械学習の数学である微積分・線形代数学・確率統計をすべて網羅して勉強することができます。
まずは数学の基礎的なところである変数・定数・関数といった内容からしっかり教えてくれます。
また、イラストや図がたくさん用いられているため、文系の読者や数学が苦手な方でもとっつきやすい本となっております。
要所に「人工知能ではこう使われる!」といったコラムがあり、機械学習に結びつけて勉強できるというのもおすすめのポイントです。
文系出身だけど機械学習に挑戦してみたい方や機械学習の数学を結びつけて勉強したい方にはうってつけの本となります。
みなさんも機械学習にチャレンジするならばぜひ数学の勉強もやっていきましょう!
最後までこの記事を読んでいただきありがとうございました!







コメント