こんにちは、かじつとむです
今まで、集合ってどういうものなのか、また集合の種類や法則について解説してきました。
今回は実際に集合の要素の個数を計算する方法について解説します。
この記事を読むことで以下のことがわかります。
- 集合の要素の個数について理解することができる
- 集合の要素の個数を計算する方法について理解できる
それではいってみましょう!
【集合の要素の個数を計算する】要素の個数による集合の分類
集合の要素の個数を計算する前に、要素の個数による集合の分類について理解しましょう!
集合の要素の数に限りがない集まりを無限集合といいます。
たとえば、1cmの線分上の点は無数に取れることから、無限集合として扱います。
一方で、集合の要素の数に限りがある集まりを有限集合といいます。
たとえば、サイコロ1つの出目は、1、2、3、4、5、6といった数に限りがあり、この集まりを有限集合として扱います。
よって、無限集合には要素の個数に限りがないためその数を数えることはできませんが、有限集合であれば要素の個数に限りがあるためその数を数えることができます。
そして有限集合Aに対する要素の個数を$ n(A) $とあらわします。
たとえば、サイコロ1つの出目の集合をAとすると、その数は全部で6個あるため$ n(A) = 6 $とあらわします。
以上が集合の要素の個数による集合の種類や、個数のあらわし方となります。
次は本題である集合の要素の個数の計算方法について解説します。
【集合の要素の個数を計算する】集合の公式
集合の公式は主に以下の2つがあります。
- 共通部分と和集合:$n(A \cup B) = n(A) + n(B) – n(A \cap B)$
- 全体集合と補集合:$n(\overline{ A }) = n(U) – n(A)$
それぞれの公式について解説します。
集合の公式 その1:共通部分と和集合
共通部分と和集合の要素の個数の公式を解説する前に、それぞれの用語についてかんたんに解説します。
共通部分とは、2つの集合A、Bに対してどちらにも属する要素すべての集合のことをいいます。
共通部分は数学的に以下のようにあらわします。
$$ 集合AとBの共通部分:A \cap B $$
よって共通部分の要素の個数は以下のようにあらわすことができます。
$$ 集合AとBの共通部分の要素の個数:n(A \cap B) $$
和集合とは、2つの集合A、Bに対してどちらか一方に属する要素すべての集合のことをいいます。
和集合は数学的に以下のようにあらわします。
$$ 集合AとBの和集合:A \cup B $$
よって和集合の要素の個数は以下のようにあらわすことができます。
$$ 集合AとBの和集合の要素の個数:n(A \cup B) $$
また、共通部分と和集合を図にあらわすと以下となります。
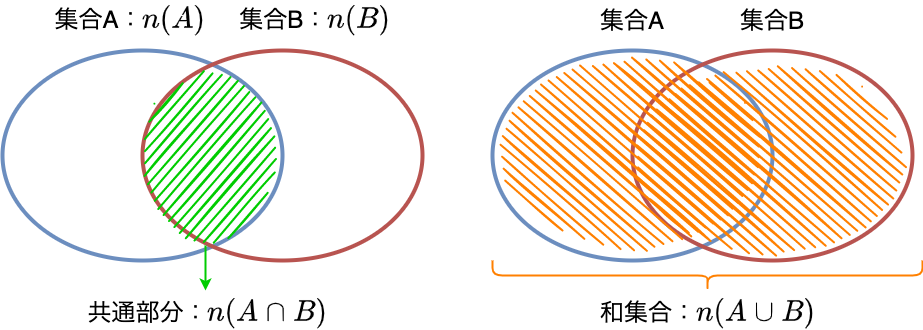
以上が共通部分と和集合のおさらいになります。
では共通部分と和集合の要素の数にはどんな関係があるのでしょうか?それは以下の関係になります。
$$ n(A \ cup B) = n(A) + n(B) – n(A \cup B) $$
重要なのは、集合AとBの要素の個数がわかっていて、共通部分もしくは和集合の要素の個数どちらかがわかっていれば、わかっていない方の集合の要素の個数を計算することができるということです。
ではなぜこの公式が成り立つのでしょうか?それを今から証明します。
まず、集合Aだけに存在する要素の個数を$x$個、集合Bだけに存在する要素の個数を$y$個、そして集合AとBの共通部分にある要素の個数を$z$個とします。
すると、集合AとBの和集合の要素の個数は集合Aだけに存在する要素の個数と集合Bだけに存在する要素の個数、そして集合AとBの共通部分の要素の個数の合計となります。
すなわち、集合AとBの和集合の要素の個数は$x + y + z$個となります。
では、集合Aの要素の個数はいくつになるでしょうか?
答えは、集合Aだけの要素の個数$x$と集合AとBの共通部分の要素の個数$z$の合計値、すなわち、$x + z$個となります。
同様に集合Bの要素の個数も、集合Bだけの要素の個数$y$と集合AとBの共通部分の要素の個数$z$の合計値となりますので、$y + z$となります。
以上より、集合AとBの和集合の要素の個数をそれぞれの集合の要素の個数であらわすと以下のようになります。
$$ \begin{eqnarray}
共通部分の要素の個数:n(A \cup B) = x + y + z \\
= x + z + y + z – z \\
= n(A) + n(B) – n(A \cap B)
\end{eqnarray}$$
以上、共通部分と和集合の要素の個数の公式となります。
集合の公式 その2:全体集合と補集合
全体集合と補集合にも、要素の個数の公式があります。その前に、全体集合と補集合についてかんたんにおさらいします。
全体集合とは、ある集合から複数の部分集合を考えるとき、そのある集合のことをいいます。
全体集合はUとあらわすため、全体集合の要素の個数も$n(U)$とあらわします。
また、全体集合Uに対して部分集合Aを考えるとき、部分集合A以外の集合をAの補集合といいます。
Aの補集合は$\overline{A}$とあらわすため、Aの補集合の要素の個数も$n(\overline{A})$とあらわします。
全体集合Uと部分集合A、Aの補集合の関係を図であらわすと以下のようになります。
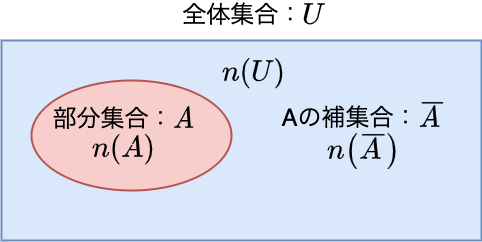
そして、全体集合Uに対して部分集合AとAの補集合には以下の関係が成り立ちます。
$$ A \cup \overline{A} = U, A \cap \overline{A} = \varnothing $$
これらを踏まえて、全体集合と補集合の要素の個数の公式を考えます。
全体集合と補集合の要素の個数の公式は以下のとおりになります。
$$ n( \overline{A}) = n(U) – n(A) $$
この公式は先ほど紹介した共通部分と和集合の関係を用いて証明することが可能です。
まず、全体集合Uに対する部分集合AとAの補集合を、共通部分と和集合の関係にあてはめると以下のようになります。
$$ n(A \cup \overline{A}) = n(A) + n(\overline{A}) – n(A \cap \overline{A}) $$
ここで、先ほどの全体集合に対する部分集合と補集合の関係を用いると上の式が以下のようにあらわすことができます。
$$ n(U) = n(A) + n(\overline{A}) – n(\varnothing) $$
ここで、空集合:$\varnothing$の要素の個数は0であるため式変形をすると以下のようになります。
$$ \begin{eqnarray}
n(U) = n(A) + n(\overline{A}) – 0 \\
n(\overline{A}) = n(U) – n(A)
\end{eqnarray}$$
よって全体集合と部分集合、補集合の関係を証明できます。
以上が、集合の要素の個数を計算するための公式となります。
【集合の要素の個数を計算する】集合の公式について:まとめ
いかがでしたでしょうか?以下まとめです。
- 集合には要素の個数が無限にある無限集合と、要素の個数に限りがある有限集合がある
- 有限集合Aの個数を$n(A)$とあらわす
- 集合AとBの共通部分と和集合の要素の個数には$n(A \cup B) = n(A) + n(B) – n(A \cap B)$という関係がある
- 全体集合Uと部分集合A、Aの補集合の要素の個数には$n(\overline{A}) = n(U) – n(A)$という関係がある
みなさんも、ぜひ集合の要素の数を計算できるようにし、データ分析に役立ててください!
集合や確率についてもっと勉強したい方へ
先ほど紹介した集合の公式や確率についてもっと勉強したい方は、「ふたたびの確率・統計[1]確率編」がおすすめです。
この本では、集合や確率や数学的に使われる記号についても網羅的に勉強することができます。
特に、確率については基礎から大学入試レベルまでより実践的な問題を使って解説しております。
最後は、大学入試問題を使った練習問題もありますので、高校生にとってもおすすめの本となります。
集合や確率について、図解でわかりやすく、かつ丁寧に解説しておりますので、文系の方や数学が苦手だった方がもう一度勉強するにはとてもとっつきやすい本です。
もしこの本で勉強した方がいれば、ぜひ以下のリンクからどうぞ!
みなさんもぜひ集合や確率について勉強してみてくださいね!
最後までこの記事を読んでいただきありがとうございました!







コメント