こんにちは、かじつとむです。
みなさんは持っているデータについて分析したいと思ったときに、まずはじめに何をすれば良いと思いますか?
平均値をとる、グラフ化するなど色々あると思いますが、まずはじめにやるべきことはデータ全体の特徴を把握することです。そのためにヒストグラムを用います。
今回はそんなヒストグラムについて説明します。
この記事を読むことで以下のことがわかります。
- ヒストグラムを作成する目的について理解できる
- ヒストグラムの概要について理解できる
- ヒストグラムの見方について理解できる
なお、ヒストグラムの作成方法について知りたい方は、以下のリンクで紹介しておりますのでもしよろしかったらどうぞ!
それでは、いってみましょう。
ヒストグラムについて:そもそもなぜヒストグラムを作成するのか?
そもそもなぜヒストグラムを作成しなければならないのでしょうか?
答えはデータ全体の特徴によって今後のデータの処理方法が変わってくるからです。
データにはもしかしたら間違った物が含まれてしまっているかもしれません。またデータに偏りが発生しているのかもしれません。
いずれにしろデータがどのような値を含んでいるのかわからない以上、まずはデータ全体のヒストグラムを作成し、データの見える化をする必要があります。
そして見える化したヒストグラムからデータ全体の特徴を見出し、今後のデータ処理や分析をしていきます。これがデータ分析の第1歩となります。
ヒストグラムについて:ヒストグラムとは?
ヒストグラムとは、あるデータを特定の範囲に区切り、その範囲のデータの個数を棒グラフで表したものとなります。
具体例として「定額預金申請データの年齢」のヒストグラムを作成します。
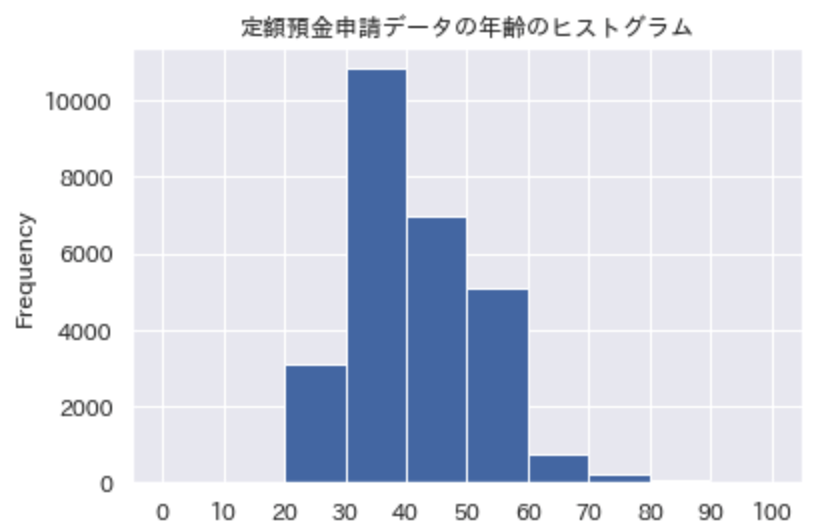
まず、年齢データを0〜10歳、10〜20歳というように10歳ずつの範囲でデータを区切り、それを横軸に表します。
次に、横軸の範囲内にあるデータの個数を数え、それを棒グラフに表すと完成となります。
今回の「定額預金申請データの年齢」のヒストグラムでは、30〜40歳のデータがもっとも集中していることがわかります。
また、30〜40歳のデータ範囲から低い年齢層よりも高い年齢層の方にデータが偏っていることを示しています。
以上2点より、定額預金申請する年齢は30歳〜40歳がもっとも集中しており、次に40歳以上の高い年齢層が定額預金申請をしていることがわかります。
このように取得したデータをヒストグラムにすることで、データの特徴を理解することができます。
ヒストグラムについて:ヒストグラムの特徴
次に、ヒストグラムの特徴について説明します。
ヒストグラムはその形状を確認することでデータの特徴を理解することができます。
では、ヒストグラムの代表的な4つの形状について紹介します。
ヒストグラムの形状1:山が1つで左右対称の形状
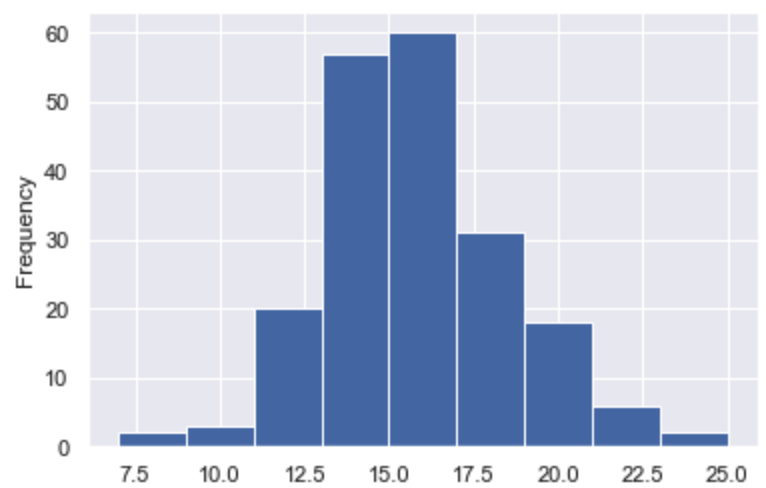
山が1つで左右対称となるヒストグラムの形状の特徴を説明します。
この場合、データの平均値、中央値、最頻値がほぼ同じ値となります。
また、新しいデータが追加された際にそのデータの値は平均値に近い値である可能性が高く、平均値から離れた値にはなりにくいこともわかります。
このようなデータの分布のことを正規分布といいます。
正規分布は自然現象や社会現象でのデータにおいてもっともよく見られる分布です。
たとえば、人間や動物の体重のデータ、学校のテストの点数のデータ、工場でつくられるものの寸法のデータも正規分布に沿ったデータの分布になるといわれております。
ヒストグラムの形状2:山が偏っているヒストグラム
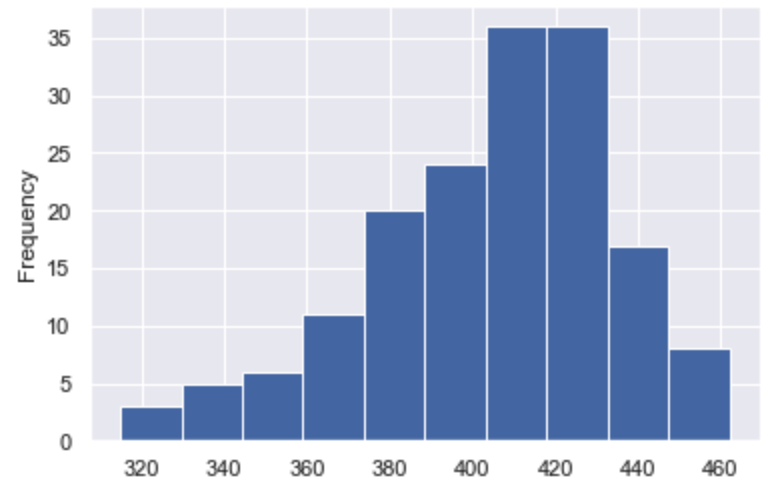
山が偏っているヒストグラムの形状の特徴を説明します。
この場合、データの値の大きい方、もしくは小さい方にデータが偏っていることがわかります。
また、データの平均値に対して、中央値および最頻値にズレが発生してしまっていることに注意が必要です。
このようなヒストグラムになった場合、現象としてこのような偏りが自然に発生してしまうのかどうか検討していく必要があります。
もし、偏りが自然に発生しない場合、データの収集方法に問題があったり、現象に課題があったりする可能性があり、これらの対策を検討していく必要があります。
偏りが自然に発生する場合、データの対数をとったり、データの加工をすることで分布を正規分布にする工夫が必要です。
ヒストグラムの形状3:山が2つあるヒストグラム
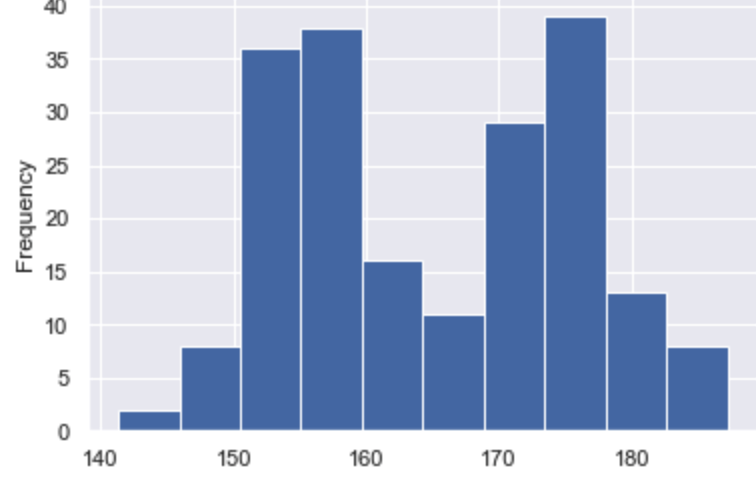
山が2つのヒストグラムの形状の特徴について説明します。
この場合、2つの異なる性質による集団のデータが混在している可能性があります。
たとえば、身長のデータであれば男性のデータと女性のデータが混在しているかもしれませんし、年齢層が異なるデータが混在しているかもしれません。
このようなヒストグラムの場合、2つの山になるデータの性質を見極めてそれぞれのデータの集団として分ける必要があります。
ヒストグラムの形状4:集団から離れた値があるヒストグラム
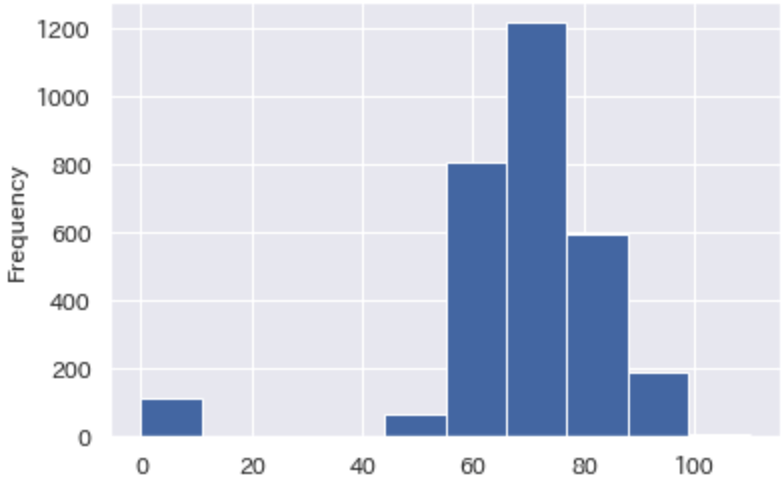
集団から離れた値があるヒストグラムの特徴について説明します。
集団から離れた値のことを外れ値といいます。本来であれば正規分布に沿ったデータの分布になるはずなのに、何らかのイレギュラーが発生したことで、外れ値をとってしまったと推定できます。
この場合、外れ値について他の値と比較して何が起こったのか、どのような違いがあるのか検討する必要があります。そして、外れ値が異常な値であるかどうかを判断する必要があります。このような異常な値である外れ値を異常値とも呼びます。
外れ値はたとえば、データの入力ミスであるとか、測定ミスがあったときに発生します。
このような外れ値は原因がわかっているならば、データ分析をする上で除外してもかまいません。また、測定ミスであったり、入力ミスであることがわかっているならば、平均値で埋め合わせる方法もあります。
ただし、外れ値にも有用な外れ値もあります。外れ値を考察することで新たな課題や発見がわかることもあります。
ヒストグラムについて:まとめ
今回はヒストグラムについて説明しました。以下まとめです。
- ヒストグラムとは、データを特定の範囲に区切り、その範囲のデータの個数を棒グラフで表したもの
- ヒストグラムの目的は、データを見える化しデータの特徴を見出すこと
- ヒストグラムの特徴は、ヒストグラムの形状を見ることで理解できる
以上です。みなさんもヒストグラムを駆使しながらデータ全体の特徴を見出してみましょう。
統計学の基礎を学びたい方へ
統計学を基礎から学びたい方へおすすめの書籍を紹介します。入門者や数学に不慣れな方で統計学を勉強するなら「完全独習 統計学入門」がおすすめです。
この本では、先ほど解説したヒストグラムの見方・考え方はもちろん、平均・分散・標準偏差といった統計学の基本的な内容を勉強することができます。
さらには、データから全体を推測する区間推定や仮説検定といった内容まで一通り網羅できるのがこの本の内容になっております。
この本では、とにかく難しい数学の話をせず、使う数学もせいぜい中学3年生までの内容で統計学を勉強できるのが特徴です。
また、各講ごとに練習問題もありますので、こちらを解くことで統計学を体感しながら学ぶこともできます。
数学は難しいけど統計学を勉強してみたい方や、統計学を初めて勉強したい方にはおすすめの一冊となります。
もしよろしければ、以下のリンクからどうぞ!
ぜひ、統計学を勉強してビジネスに活かしていきましょう!
最後までこの記事を読んできただきありがとうございました!
統計学を動画で勉強したい方はこちら!
![]()





コメント