回帰分析とは 概要から単回帰分析の方法までわかりやすく解説

こんにちは、かじつとむです。

今回は、回帰分析について解説します。

回帰分析は2つのデータの関係性を数式であらわすことができる統計学の手法となります。

また、これから機械学習を学ぶ基礎にもなるのでぜひこの機会に勉強してみましょう！

この記事を読むことで以下のことがわかります。

• 回帰分析とはどのような統計学の手法か理解できる
• 回帰分析の種類について理解できる
• 単回帰分析の方法について理解できる

もし、回帰分析をより詳しく勉強したい方は「【キカガク流】人工知能・機械学習 脱ブラックボックス講座 – 初級編 –」もおすすめです。

それではいってみましょう！

回帰分析の概要

回帰分析とは、ある変数を用いて求めたい変数を予測する関数をつくることです。

たとえば、家賃の予測をしたいとしましょう。

このとき、家の広さ・駅までの距離・間取りといった変数を使って家賃を予測するための関数をつくることが回帰分析の目的になります。

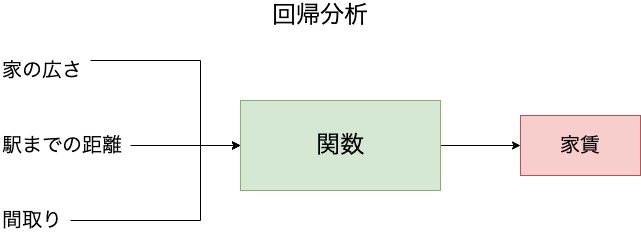
家の広さ・駅までの距離・間取りといった予測に使う変数を入力変数または説明変数といいます。

一方で、家賃のように予測したい変数のことを出力変数または目的変数といいます。

このように目的変数を説明変数を使って数式化することが回帰分析となります。

回帰分析の種類

回帰分析にはさまざまな種類があります。表にまとめると以下となります。

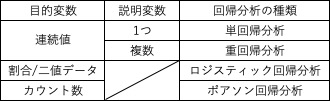
まず、目的変数が連続値であるとき説明変数の数によって種類が分かれます。

説明変数が1つである場合は単回帰分析となります。
一方で説明変数が複数である場合は重回帰分析となります。

次に目的変数が割合もしくは二値データである場合は、ロジスティック回帰分析となります。
また、目的変数がカウント数といったデータである場合は、ポアソン回帰分析となります。

このように回帰分析は色々な種類がありますが、要するにある変数を予測したいということがわかればまずはOKです。

以上が回帰分析の種類となります。
次は一番かんたんな回帰分析である単回帰分析の方法について解説します。

単回帰分析の方法

単回帰分析の方法としては以下のステップで行います。

1. 求める関数（モデル）を決める
2. 評価関数（損失関数）を決める
3. 評価関数（損失関数）を最小化する

また、この方法は重回帰分析でも適用可能です。ただしその場合には線形代数学の知識が必要になるので少し注意が必要です。

単回帰分析の方法 その1：求める関数（モデル）を決める

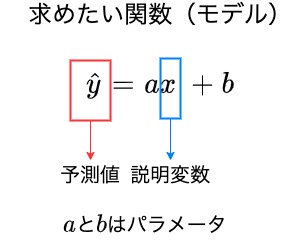
単回帰分析を行うにはまず求めたい関数を決めます。

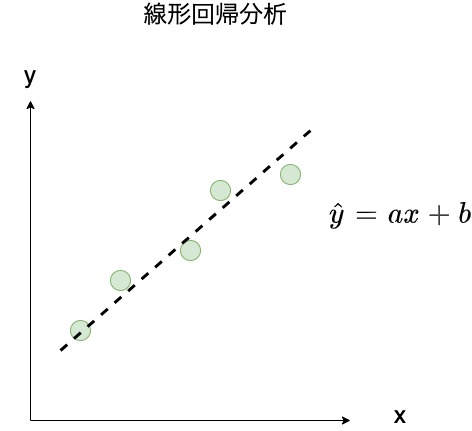
すなわち、目的変数を説明変数で予測するための直線式を説明変数の係数$a$と切片$b$を使ってあらわします。

このパラメータ$a$と$b$が最適となる条件をデータを使って決定することが、単回帰分析のゴールとなります。

ちなみに、回帰分析など予測した目的変数は$\hat{y}$で表されますので、あわせて覚えておきましょう！

今回は、単回帰分析のプロセスを理解していただくために求めたい関数を$\hat{y}=ax$とします。

単回帰分析の方法 その2：評価関数（損失関数）を決める

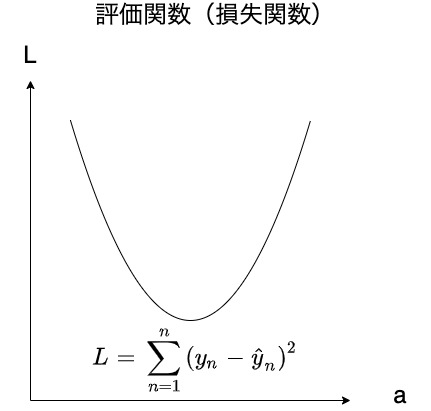
求める関数（モデル）を決めたら、評価関数（損失関数）を決めます。

評価関数（損失関数）とは、データによって得られる正解値と関数（モデル）によって得られる予測値のズレの大きさをあらわす関数です。

評価関数（損失関数）で一番使用されるのは、平均二乗誤差（MSE：Mean Squared Error） で、以下のように表します。
$$\mathrm{評}\mathrm{価}\mathrm{関}\mathrm{数}：L=\sum _{n=1}^n(y_n–{\hat{y}}_n{)}^2$$
$y_n$は各データで得られた正解値、${\hat{y}}_n$は各データの説明変数から関数（モデル）によって得られる予測値となります。

そして正解値と予測値の差を二乗した値をデータの個数$n$個で合計したものが平均二乗誤差となります。

他にも正解値と予測値の差の絶対値の合計を使う平均絶対誤差（MAE：Mean Absolute Error）などの評価関数もありますが、今回は省略させていただきます。

以上が評価関数（損失関数）を決める方法となります。

単回帰分析の方法 その3：評価関数（損失関数）を最小化する

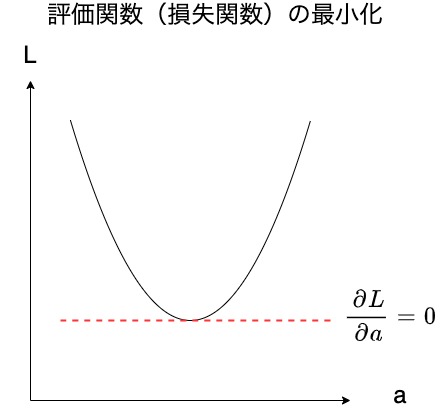
評価関数（損失関数）が決まったら、評価関数（損失関数）を最小化します。

評価関数が最小化した関数がもっとも良い予測ができている関数（モデル）であるということを示します。

では、どのように評価関数を最小化すれば良いでしょうか？

答えは、評価関数に対して求める関数の各パラメータで偏微分を行い、その値が0になるパラメータを求めることです。

では具体的に求めたい関数が$\hat{y}=ax$で、評価関数が平均二乗誤差であるときのパラメータ$a$について求めてみましょう！

まず評価関数について式変形を行うと以下のようになります。
$$\begin{array}{rcl}L& =& \sum _{n=1}^n(y_n–{\hat{y}}_n{)}^2\\ & =& \sum _{n=1}^n(y_n–a{x}_n{)}^2\\ & =& \sum _{n=1}^n(y_n^2–2x_n{y}_n+x_n^2{a}^2)\\ & =& \sum _{n=1}^n{y}_n^2-2a\sum _{n=1}^n{x}_n{y}_n+a^2\sum _{n=1}^n{x}_n^2\end{array}$$
次にこの関数をパラメータ$a$で偏微分して、その値が0となるようにすると以下のようになります。
$$\begin{array}{rcl}& \frac{\partial L}{\partial a}& =0\\ & \frac{\partial }{\partial a}& (\sum _{n=1}^n{y}_n^2-2a\sum _{n=1}^n{x}_n{y}_n+a^2\sum _{n=1}^n{x}_n^2)=0\\ & -2\sum _{n=1}^n{x}_n{y}_n& +2a\sum _{n=1}^n{x}_n^2=0\\ & a\sum _{n=1}^n{x}_n^2& =\sum _{n=1}^n{x}_n{y}_n\\ & a& =\frac{\sum _{n=1}^n{x}_n{y}_n}{\sum _{n=1}^n{x}_n^2}\end{array}$$
このように、求めたい関数のパラメータを計算します。

また、求めたい関数が$\hat{y}=ax+b$であるならば、同様の計算を行うことで以下のようにパラメータ$a,b$を計算することができます。

計算がややこしくなりますが、このようにパラメータを計算することができます。

重要なのは各パラメータで偏微分を行いその値が0となるパラメータを計算することで、予測のための関数を求めることができます。

以上が単回帰分析の方法となります。

回帰分析とは 概要から単回帰分析の方法までわかりやすく解説：まとめ

いかがでしたでしょうか？以下まとめです。

• 回帰分析とは、ある変数を用いて求めたい変数を予測する関数をつくることである
• 回帰分析の種類は、目的変数の種類や説明変数の数によってさまざまある。
• 回帰分析の方法は、求めたい関数を決める→評価関数を決める→評価関数を最小化するといった手順で行われる

みなさんもぜひ回帰分析の基礎について理解し、求めたい変数を予測してみてください！

回帰分析をより深く勉強したい方へ

回帰分析についてもっと勉強したい方は、Udemyの「【キカガク流】人工知能・機械学習 脱ブラックボックス講座 – 初級編 –」です。

この講座では機械学習やAIの概要から、1番基礎となる機械学習手法の単回帰分析について手計算やpythonでの実装する方法について教えてくれます。

機械学習の概要はもちろんのこと、機械学習に必要な基礎数学の微分やpythonの基礎までしっかり学ぶことができます。

時間は4.5時間ですので、短時間で網羅的に機械学習について理解できるところも良い点です。

面白いのはパワーポイントのようなスライド形式ではなく、紙とペンを使って手書きで教えてくれるという点です。

他の機械学習の動画講座とは違い、文字通り手を動かしながら回帰分析のメカニズムを勉強することができます。

機械学習に興味を持っている方で、数学を勉強していなかった方やプログラミングの初心者の方にもまずおすすめしたい講座となっています。

みなさんもぜひ統計学や機械学習の基礎である回帰分析を身について、よりビジネスシーンでの予測や判断に役立ててください。

最後までこの記事を読んでいただきありがとうございました！

統計学や機械学習を勉強するならスタアカもおすすめ！