こんにちは、かじつとむです。
前回、前々回と母平均を区間推定する方法について説明してきました。
今回は、母分散を区間推定する方法について説明します。
この記事を読むことで、以下のことがわかります。
- 母分散の区間推定をする方法について理解できる
- 母分散の区間推定で使われるカイ二乗分布について理解できる
それでは、いってみましょう!
母分散を推定する区間推定:結論
母分散を区間推定する方法は以下の通りです。

母分散は、標本平均$\bar{X}$、標本の数$n$、標本から得られる不偏分散$U^2$という統計量とカイ二乗分布($\chi^2$分布)を用いて区間推定をします。
不偏分散は、標本からのデータより以下の式で計算することができます。
$$ 不偏分散:U^2 = \frac{(標本のデータと標本平均の差)^2の合計}{標本の数-1} $$
不偏分散は、標本分散と計算方法が少しだけ異なり、割る数が標本の数から1引いたものになります。
不偏分散と標本分散の違いについては、点推定の記事で説明しておりますのでこちらをご参照ください。
今回新しく出てきた言葉でカイ二乗分布があります。
カイ二乗分布とは、自由度$m$によって変化する確率分布です。
自由度$m$は自由に決めることができる値の数のことをいい、標本の数から1を引くことであらわすことができる値となります。
$$ 自由度:m = 標本の数 -1 $$
自由度についてもっとよく理解したい方は、以下の記事をご参照ください。
自由度がわかったところで、母分散の区間推定に必要なカイ二乗分布についてより詳しく説明します。
母分散を推定する区間推定:カイ二乗分布($\chi^2$分布)とは
先ほども説明した通りカイ二乗分布($\chi^2$分布)とは、自由度$m$によって変化する確率分布といいました。
同様に自由度$m$によって変化する確率分布として、t分布があります。
このt分布とカイ二乗分布を比較しながら説明します。
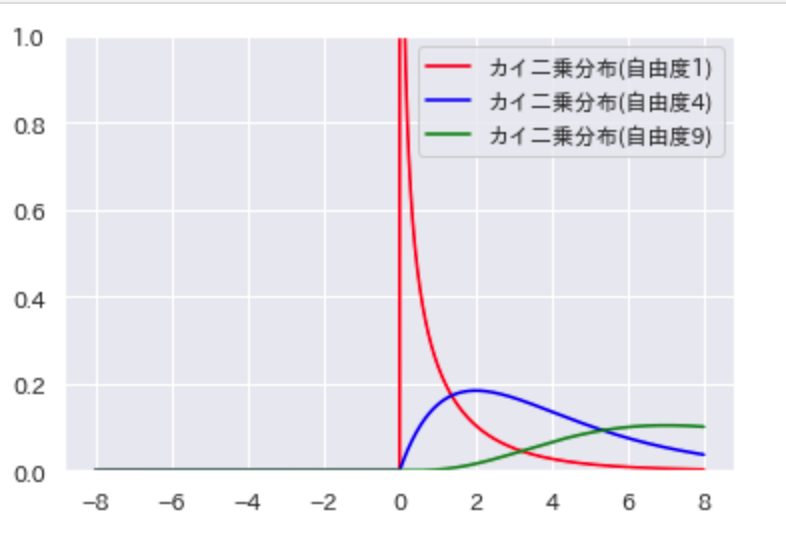
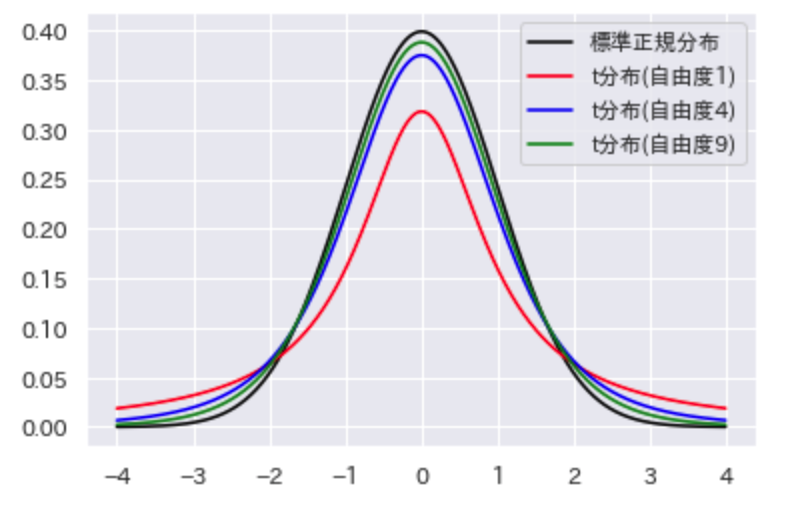
t分布とカイ二乗分布はそれぞれ以下の分布の形状になります。

カイ二乗分布 
t分布
図の左側がカイ二乗分布、図の右側がt分布および標準正規分布を示しております。
まず、カイ二乗分布は、t分布とは違い左右非対称であることがわかります。
これは、信頼区間を求めるときにとても重要です。
t分布は左右対称であるため、統計量tの信頼区間は上側パーセント点と下側パーセント点は同じ値をとります。
パーセント点とは、ある確率分布のなかで上位何%であるのか、もしくは下位何%であるのかを示す点です。
たとえば、t分布で信頼区間95%で区間推定したい場合、上側2.5%と下側2.5%の統計量t値をt分布から読みとって区間推定をします。このとき、t分布は左右対称であるため、上側2.5%と下側2.5%は同じ値になるため、読みとるべき統計量t値は1つになります。
一方でカイ二乗分布では、統計量$\chi^2$をカイ二乗分布表から、上側何%の値と下側何%の値をそれぞれ読みとって信頼区間を計算します。
たとえば、信頼区間95%で区間推定する場合、カイ二乗分布では上側2.5%の値と下側2.5%の値を読みとって信頼区間を計算するといった具合です。
このように、カイ二乗分布のような左右非対称の確率分布は、上側と下側のパーセント点をそれぞれ読みとる必要があります。
カイ二乗分布とt分布のもう1つの違いは、自由度によって確率分布の形状が大きく変わります。
自由度によって確率分布が変わるということは、標本の数によって確率分布が変わるということです。
ですので、カイ二乗分布を用いる場合は標本の数によって確率分布が変わることから、推定したい値が変わることを念頭におきましょう。
カイ二乗分布で母分散を推定するには、統計量$\chi^2$を計算する必要があります。
統計量$\chi^2$は不偏分散$U^2$、自由度$m$、母分散$\sigma^2$を使って以下のようにあらわします。
$$ \chi^2 = \frac{m \times U^2}{\sigma^2} $$
この$\chi^2$に対して、どのくらいの信頼区間で推定したいのかによって母分散を区間推定をしていきます。
では、どのように母分散を区間推定していくのか、具体例を使って説明します。
母分散を推定する区間推定:区間推定の手順
母分散の区間推定の手順について以下にまとめます。
- 推定したい標本に対して、標本平均と不偏分散を算出する
- 不偏分散、自由度、母分散$\sigma^2$を用いて、統計量$\chi^2$を算出する
- 求めたい信頼区間(何パーセントの精度)と自由度から統計量$\chi^2$の信頼区間を形成する
- 統計量$\chi^2$の信頼区間を母分散$\sigma^2$であらわす
この手順を、以下の例に当てはめながら計算していきましょう!
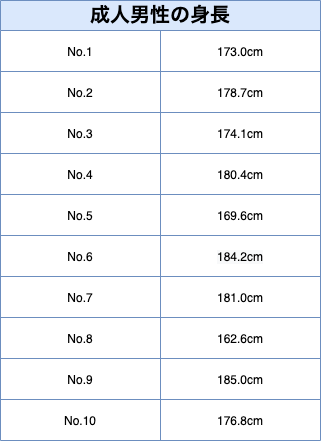
成人男性10人の身長のデータから、成人男性全体の身長の母分散を区間推定したい。
ただし、母平均がわかっていないものであり、信頼区間は95%とする。
成人男性の身長のデータは以下にあらわす。
母分散を推定する区間推定の手順 その1:標本平均と不偏分散の算出
標本のデータから、標本平均を算出します。
標本平均$\bar{X}$は以下のように算出します。
$$ 標本平均:\bar{X} = \frac{データの合計}{データの数} = \frac{173.0+178.7+\cdots+176.8}{10} = 176.54 $$
また、標本平均を使って不偏分散$U^2$を算出します。
$$ 不偏分散:U^2 = \frac{(標本のデータと標本平均の差)^2の合計}{標本の数-1} $$ $$ = \frac{(173.0 – 176.54)^2 + (178.7-176.54)^2 + \cdots + (176.8-176.54)^2}{10 – 1} = 47.86 $$
よって、不偏分散を47.86と算出することができました。
母分散を推定する区間推定の手順 その2:統計量$\chi^2$の算出
次に、統計量$\chi^2$を算出します。
まず、統計量$\chi^2$を算出するのに用いる自由度を計算します。
自由度の計算は以下の通りです。
$$ 自由度:m = 標本の数 – 1 = 10 – 1 = 9$$
よって、今回の標本の自由度は9となります。
次に、不偏分散:47.86、自由度:9、母分散$\sigma^2$を用いて統計量$\chi^2$を以下のようにあらわします。
$$ 統計量:\chi^2 = \frac{m \times U^2}{\sigma^2} = \frac{9 \times 47.86}{\sigma^2} = \frac{430.74}{\sigma^2} $$
以上のように、統計量$\chi^2$を母分散$\sigma^2$であらわすことができました。
母分散を推定する区間推定の手順 その3:統計量$\chi^2$の信頼区間の形成
次に、統計量$\chi^2$の信頼区間を形成します。
まず、求めたい信頼区間を決めます。
たとえば、90%の範囲で推定したいのか、95%の範囲で推定したいのかを決めます。
一般的に区間推定を行う場合の信頼区間は95%です。また今回の例も信頼区間は95%としているので、この信頼区間で推定します。
ただし、今までの推定とは異なり今回は信頼区間の数字が1つではありません。
理由は、カイ二乗分布が非対称の分布であるからです。非対称の分布の場合、信頼区間95%の求め方は、上側2.5%と下側2.5%のパーセント点のそれぞれの数字を用います。
以上より、求めたい信頼区間と先ほど計算した自由度が決まれば、カイ二乗分布表($\chi^2$分布表)を用いて、統計量$\chi^2$に対する信頼区間を形成します。
上側1%、2.5%、5%および下側1%、2.5%、5%のパーセント点と自由度1〜10のカイ二乗分布表は以下となります。
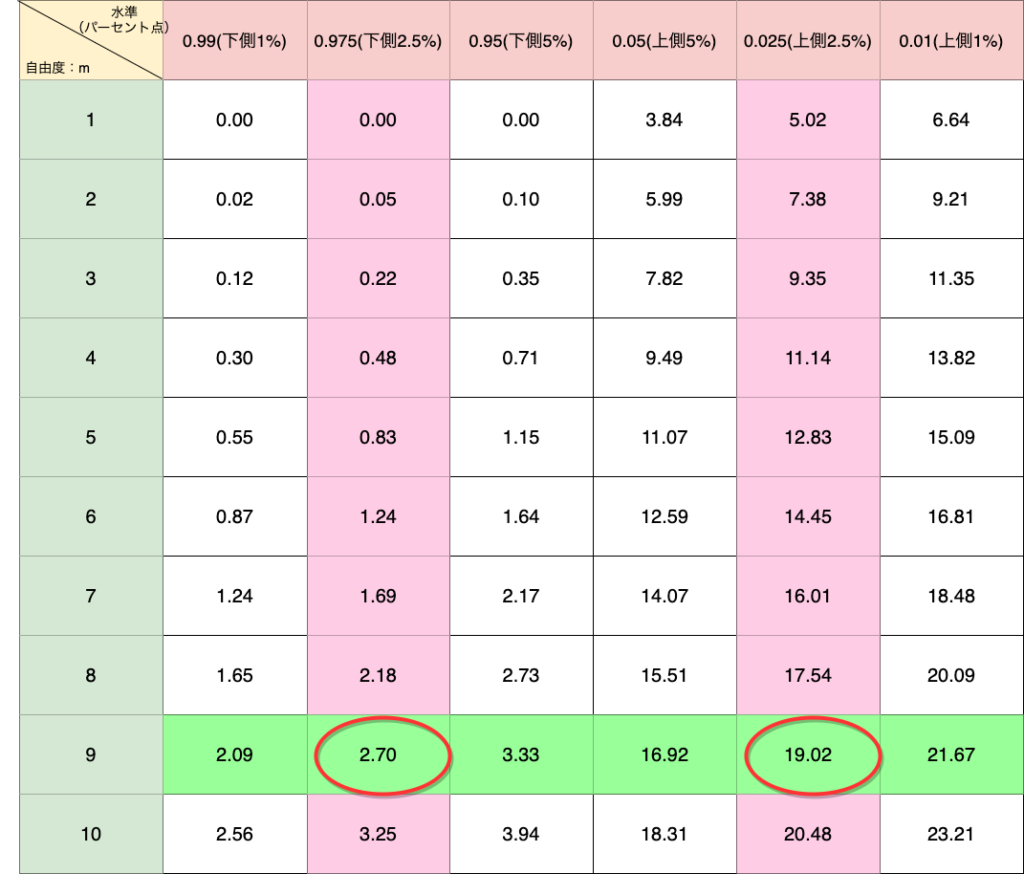
カイ二乗分布表から、求めるカイ二乗の値は自由度:9に対する、上側2.5%と下側2.5%の値を求めます。
自由度:9に対する上側2.5%の値は19.02、下側2.5%の値は2.70となります。
この数値を使って、統計量$\chi^2$に対する95%の信頼区間は以下のようにあらわすことができます。
$$ 2.70 \leq \chi^2 \leq 19.02 $$
以上より、統計量$\chi^2$の信頼区間を形成することができました。
母分散を推定する区間推定の手順 その4:統計量$\chi^2$から母分散$\sigma^2$を推定
最後は、算出した統計量$\chi^2$と統計量$\chi^2$の信頼区間から、母分散$\sigma^2$を推定します。
手順2、手順3で算出した統計量$\chi^2$と信頼区間から母分散$\sigma^2$を以下のようにあらわすことができます。
$$ 2.70 \leq \chi^2 \leq 19.02 $$
$$ 2.70 \leq \frac{430.74}{\sigma^2} \leq 19.02 $$
$$ \frac{1}{19.02} \leq \frac{\sigma^2}{430.74} \leq \frac{1}{2.70} $$
$$ \frac{1}{19.02} \times 430.74 \leq \sigma^2 \leq \frac{1}{2.70} \times 430.74 $$
$$ 22.65 \leq \sigma^2 \leq 159.53 $$
よって、成人男性の身長の分散は、95%の信頼区間で22.65cm2以上、159.53cm2以下であると推定できました。
以上が、母分散を推定する区間推定の手順となります。
母分散を推定する区間推定:まとめ
いかがでしたでしょうか?以下まとめです。
- 母分散を区間推定する場合、標本平均$\bar{X}$、標本の数$n$、標本から得られる不偏分散$U^2$から推定できる
- 母分散を推定する場合、自由度とカイ二乗分布($\chi^2分布$)を利用する
みなさんも、得られたデータから母分散の推定にチャレンジしてみてくださいね!
終わりに:統計学を勉強するおすすめの書籍
統計学を学ぶのにいくつか有用な書籍がありますが、そのなかでも入門書としておすすめの書籍を紹介します。
独学で統計学を学んでみたい方はぜひ書籍の学びにチャレンジしてみましょう!
統計学おすすめ書籍:完全独習統計学入門【小島 寛之】

この本は、データの分布を確認するヒストグラムや平均・分散・標準偏差をなるべく難しい言葉を使わずに説明しています。
そして、これらの統計量を推定する方法や母集団・標本の考え方、そして確率分布まで統計学の基礎を一通り学ぶことができる本となっております。
なんといっても、難しい数学や数式をほとんど使わずに統計学を味わうことができるのがこの本の特徴となっております。
また、各講ごとに練習問題も設定されており、これを解くことで統計学の体験もできる本です。
数学が苦手だけど統計学に興味がある方には、ぜひオススメの1冊となっております。
もしよろしければ以下のリンクからどうぞ!
ぜひ、統計学にチャレンジをして仕事に活かしていきましょうね!
最後までこの記事を読んでいただきありがとうございました!






コメント