こんにちは、かじつとむです。
前回は、確率に必要な場合の数として順列や階乗について説明しました。
今回は、もう1つの場合の数である組合せについて説明します。
この記事を読むことで以下のことがわかります。
- 組合せについて理解することができる
- 組合せの計算方法について理解することができる
それでは、いってみましょう!
確率に必要な場合の数(組合せ):順列と階乗の復習
組合せを理解するためには、順列と階乗を理解しなくてはいけません。
そのため、まずは順列と階乗の復習をしましょう!
順列とは、異なるn個のものからr個を選んで並べる場合の数のことをいいます。
n個のものからr個を選ぶときの順列は、以下の式であらわします。
$$ {}_n \mathrm{ P }_r = n \times (n-1) \times (n-2) \times \cdots \times (n-r+2) \times (n-r+1) $$
n個のものからr個を選ぶときの順列を${}_n \mathrm{ P }_r$であらわします。
このPはpermitation(パーミテーション)の略で、この単語は順列・交換・並べ替えという意味があります。
階乗とは、1からある数までの積のことをいいます。
たとえば、rの階乗は以下のようにあらわすことができます。$$ r! = r \times (r-1) \times (r-2) \times \cdots \times 2 \times 1 = {}_r \mathrm{ P }_r $$rの階乗は$ r! $または$ {}_r \mathrm{ P }_r $であらわします。
このようにあらわせることから、rの階乗はr個のものすべてを並べる場合の数であることを示しています。
順列と階乗の復習ができたことで、次は今回のテーマでもある組合せについて説明します。
確率に必要な場合の数(組合せ):組合せとは?
組合せとは、異なるn個のものからr個を選ぶ場合の数のことをいいます。
組合せが使われる例について説明します。
A, B, C, D、Eの5人のうち2人代表を選ぶときの場合の数は?
まずは、5人のうち2人を選んで並べる場合の数を樹形図であらわしてみましょう。
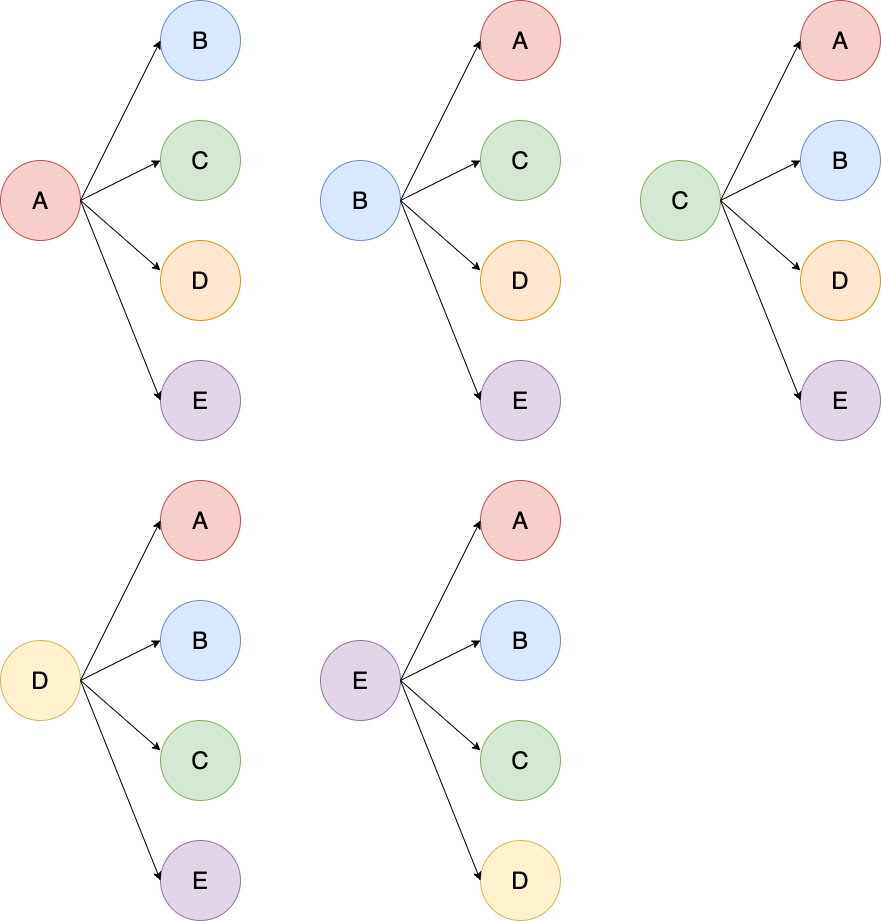
次に、選んで並べたものの中から同じ種類の人を選んでいるものを削除していきます。
たとえば、A→BとB→Aは同じものとして1つとするため、片方を削除するということです。
同じ種類の選択を削除した樹形図を以下に示します。
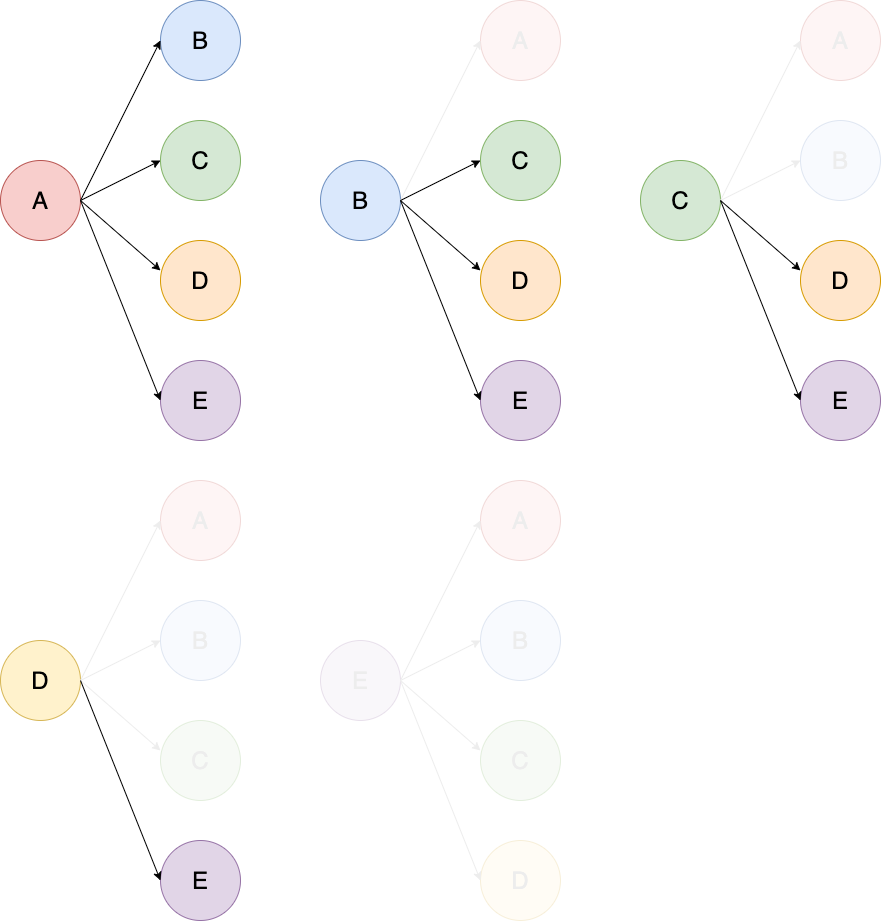
このようにあらわすことで、5人から2人を選ぶ組合せを数えることができます。
よって、5人から2人を選ぶ組合せは10通りとなります。
では、組合せについての計算式について考えてみましょう。
まず、n個からr個を選ぶ組合せを$ {}_n \mathrm{ C }_r $とあらわします。
このCはcombination(コンビネーション)をあらわしており、文字通り組合せという意味です。
組合せを計算するためには、組合せと順列・階乗の関係性を利用して計算します。
つまり、n個からr個を選び、それを並びかえたときn個からr個を選んで並べる場合の数をあらわすことができるという関係性です。
数式にすると、以下のようにあらわすことができます。
$$ {}_n \mathrm{ C }_r \times r! = {}_n \mathrm{ P }_r $$$$ n個からr個を選ぶ組合せ \times r個のものを並べる階乗 = n個からr個を選んで並べる順列 $$
よって、n個からr個を選ぶ組合せは以下のように計算することができます。
$$ {}_n \mathrm{ C }_r = \frac{{}_n \mathrm{ P }_r}{r!} $$
すなわち、n個からr個を選ぶ組合せは、n個からr個を選んで並べる順列をrの階乗で割ることで計算することができます。
では、先ほどの例、5人から2人を選ぶ組合せを計算しましょう。
$$ {}_5 \mathrm{ C }_2 = \frac{{}_5 \mathrm{ P }_2}{2!} = \frac{5 \times 4}{2 \times 1} = 10通り $$
よって、樹形図で数えた組合せと同じ10通りを計算することができました。
確率に必要な場合の数(組合せ):組合せの公式
最後に組合せを計算する上で便利な公式を1つ紹介します。それが以下の公式になります。
$$ {}_n \mathrm{ C }_r = {}_n \mathrm{ C }_{n-r} $$
これは、n個からr個選ぶ組合せはn個からn − r個を選んで残す組合せと同じということです。
先ほどの例でいうと、5人から2人を選ぶ組合せは5人から3人を選んで残す組合せと同じという意味です。実際に計算すると以下になります。
$$ {}_5 \mathrm{ C }_2 = {}_5 \mathrm{ C }_3 = \frac{{}_5 \mathrm{ P }_3}{3!} = \frac{5 \times 4 \times 3}{3 \times 2 \times 1} = 10通り $$
よって、5人から2人を選ぶ組合せと5人から3人を選んで残す組合せは同じ10通りであることがわかります。
なぜ、この公式が大切なのでしょうか?答えは、組合せを計算する上でrの数が小さければ小さいほど簡単になるからです。
先ほどの例で考えると、${}_5 \mathrm{ C }_3$を計算する場合と${}_5 \mathrm{ C }_2$を計算する場合では、${}_5 \mathrm{ C }_3$の方が計算過程が少し複雑になります。
この例では2が3になるだけですが、もっと大きい数字であればより複雑な計算をしなければなりません。
ですので、$ {}_n \mathrm{ C }_r = {}_n \mathrm{ C }_{n-r} $の公式は計算過程を簡単にする上で重要な公式ともいえます。
確率に必要な場合の数(組合せ):まとめ
いかがでしたでしょうか?以下まとめです。
- 組合せとは、異なるn個のものからr個を選ぶ場合の数である
- 組合せは、順列と階乗を利用して計算することができ、その式は${}_n \mathrm{ C }_r = \frac{{}_n \mathrm{ P }_r}{r!}$である。
- 組合せの公式の1つに$ {}_n \mathrm{ C }_r = {}_n \mathrm{ C }_{n-r} $があり、これは計算過程を簡単にする便利な公式である
みなさんも、順列と組合せの違いを理解しながら確率の理解の第一歩を踏み出してみてください!
最後までこの記事を読んでいただきありがとうございました!




コメント