こんにちは、かじつとむです。
少し前に母集団と標本について解説しました。
今回は、実際に標本から母集団を推定する方法の1つ点推定について説明します。
この記事を読むことで以下のことがわかります。
- 標本から母集団を推定する方法がわかる
- 推定するために必要な統計学の用語や数式を理解できる
それでは、いってみましょう!
母集団と標本とは
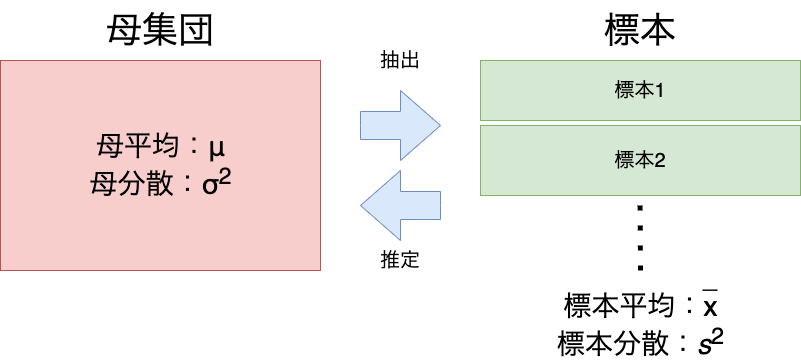
母集団とは、調査対象すべてのデータのことです。
たとえば、日本人全員の給料の母集団は文字通り日本人すべての人の給料となります。
標本とは、調査対象から一部を抽出したデータのことです。
先ほどの例で示した日本人全員の給料の標本は、「日本人1人の給料」「日本人1000人の給料」などがあげられます。
母集団と標本には、それぞれ基本統計量を持っています。
基本統計量とは、データ分布の特徴を1つの数値で表す指標のことです。
母集団の基本統計量は母平均と母分散です。
母平均は、母集団の平均値のことです。計算方法は以下となります。
$$ 母平均:\mu = \frac{母集団のデータの合計}{母集団のデータの数} $$
母平均は母集団のデータの合計から母集団のデータの数で割れば計算できます。
また、母平均は記号で$\mu$(ミュー)とあらわします。
母分散は、母集団の分散のことです。計算方法は以下となります。
$$ 母分散:\sigma^2 = \frac{(母集団のデータと母平均の差)^2の合計}{母集団のデータの数} $$
まず、母集団の1つのデータに対して母平均との差を出します。
その後、それぞれの母集団のデータと母平均の差を二乗します。
2乗したデータを母分散のデータの数で割れば、それが母分散となります。
また、母分散は記号で$\sigma^2$(シグマにじょう)とあらわします。
これらの母平均・母分散は総称として母数ということもあるので覚えておいてください。
一方で標本の基本統計量は標本平均と標本分散です。
標本平均と標本分散は、母平均・母分散と同様に以下の方法で計算できます。
$$ 標本平均:\bar{ x } = \frac{標本のデータの合計}{標本のデータの数} $$
$$ 標本分散:s ^2= \frac{(標本のデータと標本平均の差)^2の合計}{標本のデータの数} $$
また、標本平均・標本分散は記号で$\bar{ x }$(エックスバー)・$s^2$とあらわします。
これらの標本平均・標本分散は推定量ということもあるので覚えておいてください。
母集団から抽出したものを標本といいます。
一方で標本から母集団を推定することができます。
これが統計学の目的です。
ところで、推定とは何でしょうか?次は推定やその方法について説明します。
推定とは? 推定の概要や種類
統計学的な推定の意味を辞書で引くと以下のようになります。
統計調査で、ある集団の性質を調べる場合に、その集団から抽出した標本を分析することによって集団全体の性質を判断すること。
https://www.weblio.jp/content/%E6%8E%A8%E5%AE%9A
要するに、標本を分析することで母集団の性質を導くことです。
母集団のデータを1つ1つすべて調べ上げて、その性質を確認することは時間的にも労力的にも大変難しいです。
よって、母集団から抽出された標本を使って母集団の性質を考えることは自然な考えとなります。
では具体的にどのように推定するのでしょうか?
答えは標本から計算した推定量を用いて母数の値を絞り込むことです。
そのために、標本から標本平均や標本分散を計算する必要があります。
標本平均や標本分散を使って、母平均や母集団を予測するっていうのが推定の流れです。
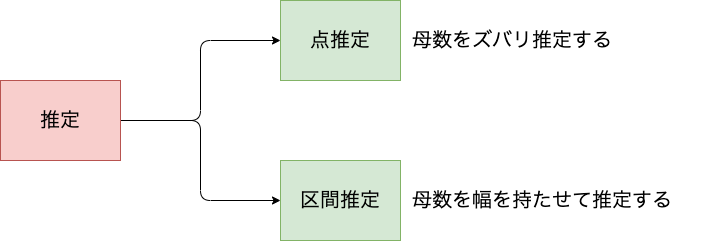
また、母集団を推定する方法は大きくわけて2つあります。それは、点推定と区間推定です。
点推定とは、母数をズバリ推定する方法です。
これは、標本から標本平均と標本分散の計算方法利用して、母平均と母分散を推定します。
一方で区間推定とは、母数を幅を持たせて推定する方法です。
これは母平均が〇〇〜△△の幅で何%の確率で入っているのかを計算します。
この場合、標本平均と標本分散の計算に加えて確率変数を使って母平均の幅を計算します。
今回は、点推定について説明します。
点推定の方法
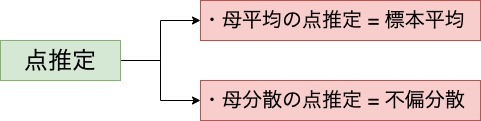
母平均と母分散を点推定で計算する方法を説明します。
まず、実際に母集団と標本のデータをとったときの例を考えてみます。
母集団は平均値が200の分散が400のランダムなデータが5000個とします。
そして、その中のデータをランダムに1000個抽出したデータを標本とします。
上記で定義した母集団と標本をそれぞれヒストグラムに表すと以下のようになります。
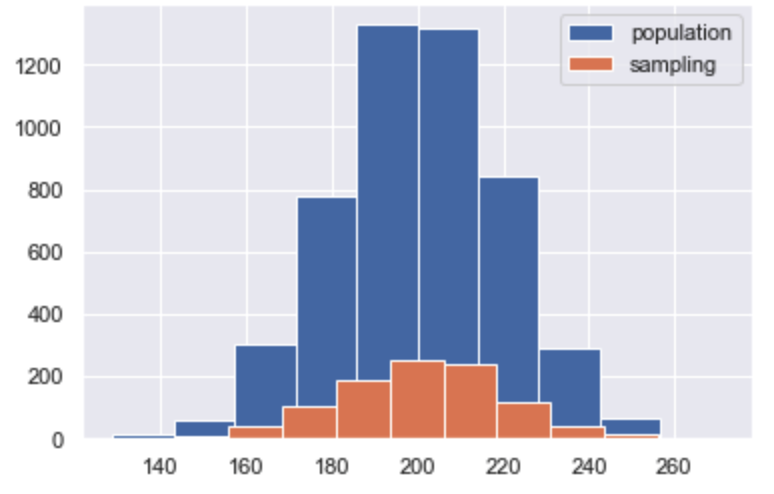
図では青のヒストグラムが母集団、オレンジのヒストグラムが標本となります。
まず、母集団と標本のヒストグラムの山が大きくなるところはほぼ一致していることがわかります。
すなわち、標本の平均は母集団の平均とほぼ一致しているということがわかります。
一方で、母集団と標本のヒストグラムの広がりは、標本の方が母集団に比べてやや狭いことがわかります。
すなわち、標本の分散は母集団の分散に比べると小さいことがわかります。
以上を踏まえて母平均・母分散の点推定の方法を説明します。
母平均は標本平均を計算すれば推定できることがわかります。
$$ 母平均 = 標本平均 $$
なぜなら、母集団と標本のヒストグラムは大きさは違えどほぼ同じ形状になるからです。
上記のヒストグラムでもわかるように、大きさは違うが形状は同じ、特にヒストグラムが一番高くなる周辺の数値はほぼ同じであることがわかります。
一方で、母分散は標本分散を計算しても推定することはできません。
理由はヒストグラムの大きさが違うからです。
標本は母集団に比べヒストグラムは小さいため、標本分散は母分散に比べ小さくなってしまいます。
では、どうすれば標本から母分散を推定できるのでしょうか?
答えは標本から不偏分散を計算することです。
不偏分散は標本を使って以下のように計算できます。
$$ 不偏分散:U^2= \frac{(標本のデータと標本平均の差)^2の合計}{標本のデータの数 − 1} $$
標本分散とほぼ同じですが、割る値が標本のデータの数から−1したものになっています。
また、不偏分散は英語でUnbiased varianceということから$ U^2 $と表します。
この不偏分散が母分散として推定する値となります。
$$ 母分散 = 不偏分散 $$
なぜ標本分散ではなく、不偏分散で推定するのでしょうか?
答えは、不偏分散は標本分散よりも大きくすることができ、かつ、母集団の性質を表すことができるからです。
標本分散の問題点は標本よりも母集団の方が大きいために、母分散を過小評価してしまうことでした。
そこで、その過小評価分を不偏分散を使うことで補い推定しているということです。
実際の計算式で考えると以下になります。
$$ 不偏分散 = 標本分散 \times \frac{標本のデータの数}{標本のデータの数 − 1} $$
この式から不偏分散の方が標本分散より(標本のデータの数)/(標本のデータの数 − 1)だけ大きくなることがわかります。
このように標本分散を少し補正した不偏分散を使って母分散を推定します。
標本から母集団を推定しよう!(点推定):まとめ
いかがでしたでしょうか?以下まとめです。
- 推定とは、標本を分析することで母集団の性質を導くこと
- 推定は、母集団の性質ズバリの値を推定する点推定と幅を持たせて推定する区間推定がある
- 点推定の場合、母平均は標本平均を、母分散は不偏分散を計算することで推定できる
みなさんも、データから全体の性質を読み取りたい場合はぜひ点推定を使ってみてください!
標本から母集団を推定する統計学をもっと勉強したい方へ

統計学の入門者で、基礎から実際に値を推定するところまで勉強したい方におすすめなのは「完全独習 統計学入門」です。
この本では、データの特徴をあらわす記述統計学からデータの予測をする推測統計学まで一通り勉強することができます。
具体的には、先ほど勉強したヒストグラムや平均・分散・標準偏差といった基本統計量の使い方、さらには統計量を推定する方法を勉強できます。
この本の特徴は、難しい数学や数式をほとんど使っておりませんのではじめて統計学を勉強する方でもとっつきやすい本です。
また、各講ごとに練習問題もありますので、こちらを解くことで統計学を体感することもできます。
統計学を初めて勉強したいと思った人や数学が苦手だけど統計学を学びたい方には、おすすめの一冊となります。
皆さんもぜひデータの推定ができるように統計学を勉強していきましょう!
最後までこの記事を読んでいただきありがとうございました!
統計学から機械学習までガッツリ動画で学びたい方はUdemyの「【世界で37万人が受講】データサイエンティストを目指すあなたへ〜データサイエンス25時間ブートキャンプ〜
![]() 」がおすすめ
」がおすすめ





コメント