こんにちは、かじつとむです。
今までは1つの母集団に対しての検定方法について解説していきました。
今回は2つの母集団を検定する方法、F検定について解説します。
F検定は製造業の品質管理でもっとも使われる統計分析方法の1つです。
また、分散分析や実験計画法といったより複雑な統計分析方法の基礎となる部分でもありますので、みなさんもぜひこの記事を読んで勉強しましょう!
この記事を読むことで以下のことがわかります。
- F検定とはどのような検定方法なのか理解できる
- F検定で使う確率分布、F分布について理解できる
- F検定のやり方について理解できる
それではいってみましょう!
F検定とは:F検定の概要
F検定とは、2つの母集団に対しその母分散を比較する検定方法です。
すなわち、2つの母集団のばらつきに違いがあるかどうかを調べます。
具体的には、まずばらつきの違いを調べたい2つの独立した母集団を設定します。
それぞれの母集団が正規分布でデータが分布していると仮定し、母平均:$\mu_{1}, \mu_{2}$、母分散:$\sigma^2_{1}, \sigma^2_{2}$とし、母集団からとった標本の数を$n_{1}, n_{2}$、不偏分散を$V_{1}, V_{2}$とします。
次に、統計量$F$を以下の式で計算します。
$$ F = \frac{\require{physics} \flatfrac{V_{1}}{\sigma^2_{1}}}{\flatfrac{V_{2}}{\sigma^2_{2}}}$$
この統計量$F$が、自由度($n_{1}-1, n_{2}-1$)のF分布という確率分布に従います。
これを利用して、統計量$F$とF分布からもとまる信頼区間を比較することで、ばらつきの違いを確認する方法がF検定です。
F検定は製造業の中でも数多くの事例で使われています。
たとえば、2拠点の工場の品質の差のありなしや、新しい材料にしたときに品質が向上したかどうかといった違いを調べるために使われています。
以上がF検定の概要です。次はF検定をする際に使われる確率分布、F分布について解説します。
F検定とは:F分布とは
先ほども説明した通りF分布とは、2つの自由度($n_{1}-1, n_{2}-1$)によって変化する確率変数です。F分布は以下の分布の形状になります。
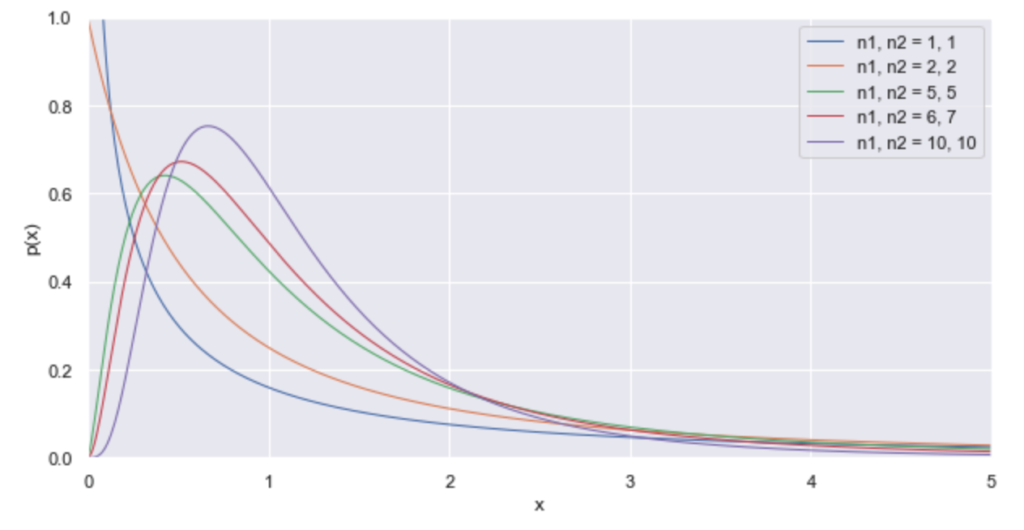
まず、F分布は左右非対称の分布であることがわかります。
これは検定を行う際に信頼区間が上側と下側でそれぞれ異なることを示します。
たとえば、信頼区間95%でF検定を行う場合、F分布から上側2.5%の値と下側2.5%の値を読み取って信頼区間を求めます。
また、信頼区間を求める場合はF分布表を使うのが一般的です。
F分布表は有意水準と2つの自由度($n_{1}-1, n_{2}-1$)を使って、有意水準に対する統計量$F$を計算する表です。
たとえば、有意水準を0.975(上側2.5%)のとき2つの自由度($n_{1}-1, n_{2}-1$)を1〜10まで振った値の統計量$F$は以下の表であらわすことができます。
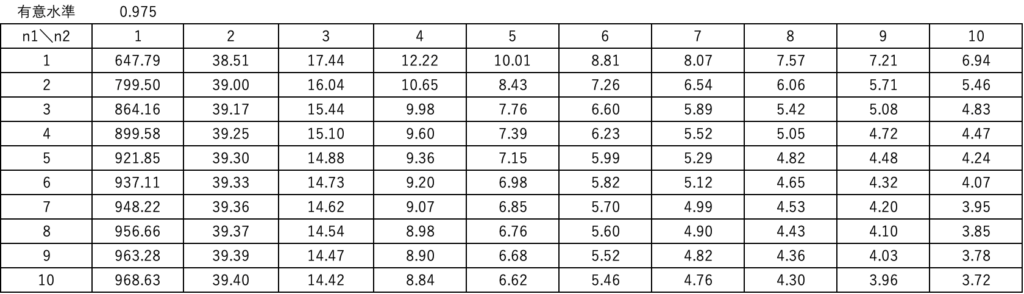
このようにF分布表を用いて信頼区間を求め、実際に計算した統計量$F$を比較することでF検定を行うことができます。
F分布にはもう1つ重要な性質があります。
その性質は以下のような計算式が成り立つことです。
$$ F(n_{1}-1, n_{2}-1, \alpha) = \dfrac{1}{F(n_{2}-1, n_{1}-1, 1 – \alpha)} $$
ここで$\alpha$は分布であらわす確率となります。
この式を利用することで1つのF分布表だけでF検定を行うことができるようになります。
たとえば、2つの母集団に対して1つの標本の自由度が8、もう1つの標本の自由度が4で信頼区間95%でF検定を行う場合を考えましょう。
まず上側2.5%の統計量$F$を計算するため、有意水準0.975のF分布表から読み取ります。
$$ F(8, 4, 0.975) = 8.98 $$
次に下側2.5%の統計量$F$を計算するのですが、このときに先ほどの式を利用することができます。
つまり、自由度を逆にして有意水準0.975のF分布表を読み取ることで計算することができます。
$$ F(8, 4, 0.025) = \dfrac{1}{F(4, 8, 0.975)} = \dfrac{1}{5.05} = 0.198 $$
よって2つの母集団に対して1つの標本の自由度が8、もう1つの標本の自由度が4で信頼区間95%でF検定を行う場合、標本から得られる統計量$F$が0.198〜8.98の間にあるかどうかを調べれば良いということになります。
以上がF分布の概要および性質となります。次は実際の問題を使ってF検定の手順を解説します。
F検定とは:F検定の手順
F検定は以下の手順で行います。
- 帰無仮説と対立仮説を設定する
- 2つの標本の不偏分散と自由度を計算する
- 有意水準を決める
- 対立仮説から有意水準に応じた棄却域を決める
- 不偏分散から統計量Fを計算する
- 統計量と棄却域を比較し、帰無仮説を棄却するか判断する
この手順を以下の例を用いて解説します。
ある2つの工場では、同じ製品で同じ硬さの保証を行っている。2つの工場での製品の硬さは同じばらつき具合であることが望ましい。よって2つの工場での製品の硬さのばらつき具合を比較することにした。工場Aから7個、工場Bでは6個の硬さのデータを取得し以下の結果が得られたとき、ばらつきは同じであるか確認する。
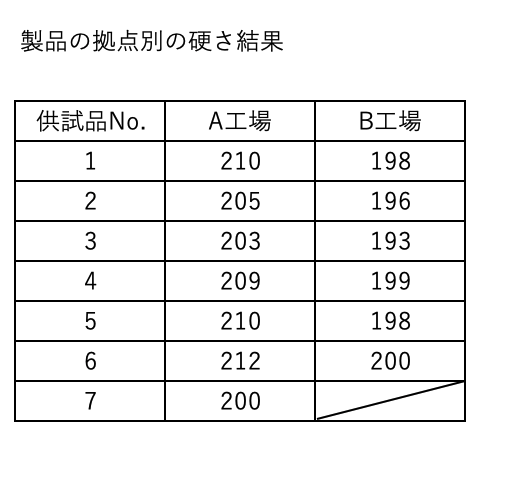
F検定の手順 その1:帰無仮説と対立仮説を設定する
まず、帰無仮説と対立仮説を設定します。
今回は工場Aと工場Bの硬さのばらつきが違うのではないかということを考えていますので、帰無仮説と対立仮説は以下のように設定します。
- 帰無仮説:工場間での硬さのばらつきは同じ
- 対立仮説:工場間での硬さのばらつきが違う
このように、帰無仮説は自分の否定したい仮説のことをいい、対立仮説は自分で考えたり感じたりした仮説を立てます。
F検定の手順 その2:2つの標本の不偏分散と自由度を計算する
帰無仮説と対立仮説を設定したら、2つの標本の不偏分散と自由度を計算します。
不偏分散は以下の式から算出します。
$$ 不偏分散:V = \dfrac{(標本データと標本平均の差)^2の合計}{標本の数 – 1} $$
よってそれぞれの工場の不偏分散は以下のようになります。
$$ V_{A工場} \fallingdotseq 19.33 $$ $$ V_{B工場} \fallingdotseq 6.27 $$
自由度は以下の指揮から算出します。
$$ 自由度:\phi = 標本の数 – 1 $$
よってそれぞれの工場の自由度は以下のようになります。
$$ \phi_{A工場} = 7-1 = 6$$ $$ \phi_{B工場} = 6-1 = 5$$
以上のように不偏分散と自由度を計算しておきます。また、不偏分散の大小関係は棄却域を決めるのに重要なので押さえておきましょう。
F検定の手順 その3:有意水準を決める
不偏分散と自由度を計算したら、有意水準を決めます。
有意水準は一般的に5%か1%となります。
今回は有意水準を5%の設定します。
F検定の手順 その4:対立仮説から有意水準に応じた棄却域を決める
有意水準を決めたら、対立仮説に応じて棄却域を決めます。
今回のようにばらつきが違うという対立仮説の場合には、標本の不偏分散同士の大小関係によって以下のように棄却域と統計量$F$を決めます。
$$ V_{1} \geq V_{2}のとき、統計量:F = \dfrac{V_{1}}{V_{2}} \geq F(\phi_{1}, \phi_{2}, \frac{\alpha/2}{2}) $$ $$ V_{1} \lt V_{2}のとき、統計量:F = \dfrac{V_{2}}{V_{1}} \geq F(\phi_{2}, \phi_{1}, \frac{\alpha/2}{2}) $$
このようにばらつきが違うという対立仮説の場合は、標本の不偏分散同士の大小関係によって棄却域や求める統計量が変化することに注意しましょう。
また、どちらか一方のばらつきが大きい(小さい)といった対立仮説の場合には、以下のように棄却域と統計量$F$を決めます。
対立仮説:標本1よりも標本2の方がばらつきが大きい場合
$$ 統計量:F = \dfrac{V_{2}}{V_{1}} \geq F(\phi_{2}, \phi_{1}, \alpha) $$
対立仮説:標本1よりも標本2の方がばらつきが小さい場合
$$ 統計量:F = \dfrac{V_{1}}{V_{2}} \geq F(\phi_{1}, \phi_{2}, \alpha) $$
以上のように対立仮説によって棄却域を決めていきます。
F検定の手順 その5:不偏分散から統計量を計算する
棄却域を決めたら、不偏分散から統計量$F$を計算します。
今回の例では、2つの工場間でばらつきが違うという対立仮説であること、また不偏分散の大小関係が$V_{A工場} \geq V_{B工場}$であることから以下のように統計量$F$を計算します。
$$ 統計量:F = \dfrac{V_{A工場}}{V_{B工場}} = \dfrac{19.33}{6.27} \fallingdotseq 3.08 $$
このように対立仮説と不偏分散の大小関係から統計量$F$を計算します。
F検定の手順 その6:統計量と棄却域を比較し、帰無仮説を棄却するか判断する
統計量$F$を計算したら、棄却域と比較し帰無仮説を棄却するか判断します。
棄却域は対立仮説で設定した値を、F分布表から読み取ることで定めることができます。
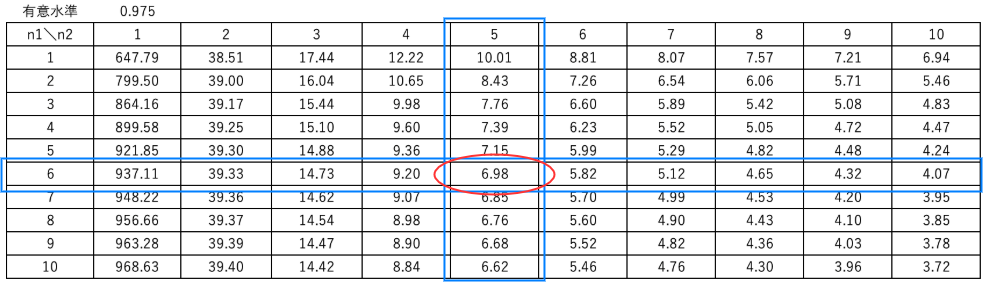
$$ F(\phi_{A工場}, \phi_{B工場}, 0.975) = 6.98 $$
この値と先ほど計算した統計量$F$を比較します。
$$ 統計量:F \fallingdotseq 3.08 \lt 6.98 $$
よって統計量$F$よりも棄却域の方が大きいことから帰無仮説は棄却できない、すなわち工場間での硬さのばらつきは同じであることがいえます。
以上がF検定の手順となります。
【徹底解説】F検定とは F分布からF検定の使い方まで解説:まとめ
いかがでしたでしょうか?以下まとめです。
- F検定とは、2つの母集団に対しその母分散を比較する検定方法である
- F検定で計算する統計量Fは、2つの母集団の標本から不偏分散を計算し、その比を求めることであらわされる
- F分布は統計量Fに対する確率変数であり、2つの標本から得られる自由度によって変化する
- F検定は、帰無仮説の立て方や不偏分散の大小関係が重要で、これらによって計算すべき統計量と棄却域が変化する
みなさんもぜひこの記事を読んで、F検定にチャレンジしてみましょう!
F検定などの統計学をもっと勉強したい方へ
先ほど紹介したF検定を含めた統計学をもっと勉強したい方は「入門 統計解析法」がおすすめです。
この本では、分散や標準偏差などの基本的内容から仮説検定・分散分析・回帰分析といった製造業の現場で実践的に使える統計学について学ぶことができます。
高校数学の内容までの数式を使いますが、実際の製造業で使われる具体例を用いて統計学を解説しておりますので、使い方をイメージできる一冊となります。
数学の知識を持っており、実務で使える本格的な統計学を学びたい方にはぜひおすすめの本です!
ただしこちらの本を手に取ってみて、難しいと感じた場合は「完全独習 統計学入門」がおすすめです。
どちらも統計学を勉強するにはおすすめの本ですので、みなさんもぜひ統計学の勉強をして行ってみましょう!
最後までこの記事を読んでいただきありがとうございました!
統計学を動画で勉強したい方はこちら
![]()





コメント