こんにちは、かじつとむです。
Excelのデータ分析について前回は、データ分析をかんたんに実現するためのツールの導入方法について解説しました。
今回は、Excelのデータ分析の第一歩として基本統計量の計算方法について解説します。
この記事を読むことで以下のことがわかります。
- Excelで基本統計量の算出の仕方がわかる
- Excelでの関数の使い方について理解できる
それではいってみましょう!
Excelで基本統計量を計算する方法:Excelの関数とは
Excelで基本統計量を算出する前に、どのような仕組みで算出できるのかについて解説します。
これは、Excel内部に組み込まれている関数を使って算出します。
Excelでいう関数とは、求めたい計算をかんたんに行うための機能です。
たとえば、123個のデータの平均値を計算する場合を考えてみましょう!
この場合は、まず123個のデータを1つ1つ全部足し合わせ、それからデータの個数分、すなわち123で割るという計算を行います。
この計算を手で行うと非常に手間ですし、平均値より複雑な標本分散や標準偏差などを計算する場合、もっと大変な作業になることは明白です。
よって、このような複雑な計算をかんたんに行うため、Excelでは使用頻度の高い統計量を計算するための関数が用意されております。
では具体的にExcelでどのように関数を使えば良いか説明します。
具体的に説明するため、以下のデータを用います。
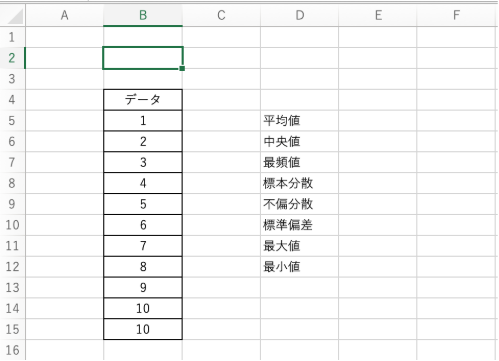
このデータはB5〜B15のセルに記載されている状態です。
まず関数を用いて計算する場合は、計算結果を表示したいセルを選択します。
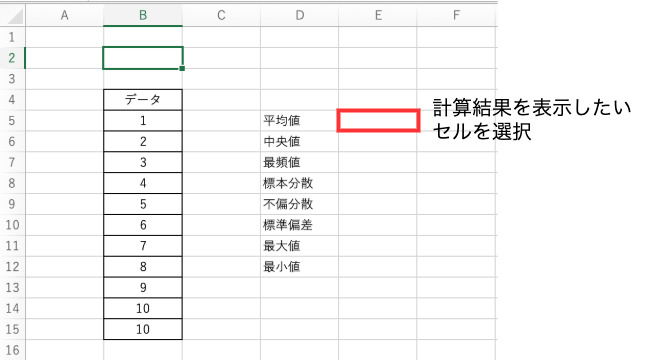
続いてこのセルのなかに以下のような形で関数名と引数(関数を適用するデータの値)を入力します。
$$ \mathsf{=関数名(引数)} $$
少しわかりづらいと思うので上記のB5〜B15セルの平均値を計算する場合は以下のように入力します。
$$ \mathsf{=AVERAGE(B5:B15)} $$
まず、AVERAGEというのが平均値を計算するための関数となります。
そして、B5:B15というのはB5からB15までの値を使って計算するという意味となります。
具体的にExcelシート内での作業としては以下のようになります。

最後に関数を入力した状態でEnterキーを押すと、関数によって計算された値がセル内に表示されます。
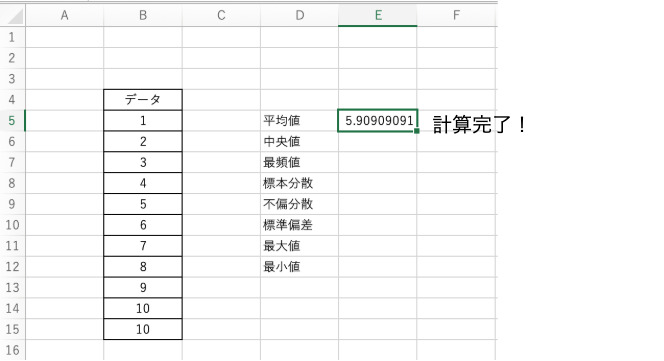
以上がExcelでの関数の使い方になります。では次にExcelの関数を使った基本統計量の計算方法について解説します。
Excelで基本統計量を計算する方法:関数を使った基本統計量の計算
それではExcelを使った基本統計量の計算方法について解説します。
今回解説する基本統計量は以下の8つです。
- 平均値
- 中央値
- 最頻値
- 標本分散
- 不偏分散
- 標準偏差
- 最大値
- 最小値
それぞれの基本統計量の計算方法について解説します。
関数を使った基本統計量の計算 その1:平均値
平均値とはデータの合計をデータの数で割ることで得られる値です。
平均値はデータの中心的な値であり、データの範囲内に存在します。
平均値を計算するための関数は上記でも説明した通り以下となります。
$$ \mathsf{=AVERAGE(引数)} $$
先ほどの例に対してB5〜B15までのセルのデータの平均値を算出する場合、以下のように関数を適用します。
$$ \mathsf{=AVERAGE(B5:B15)} $$
以上のように関数を組み込むことで平均値を算出することができます。
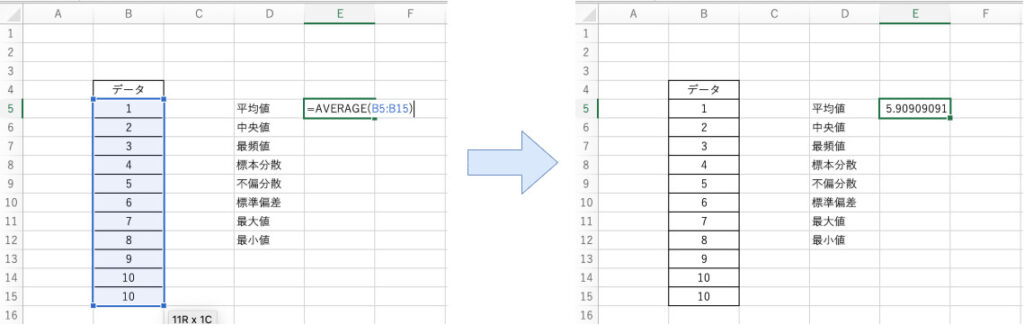
関数を使った基本統計量の計算 その2:中央値
中央値とは、データを小さい順に並べて、データの数によって以下の定義によってあらわされる統計量です。
- データが奇数個ならば、中央に位置するデータの値
- データが偶数個ならば、中央に位置する2つのデータの平均値
中央値をExcelで計算する関数は以下となります。
$$ \mathsf{=MEDIAN(引数)} $$
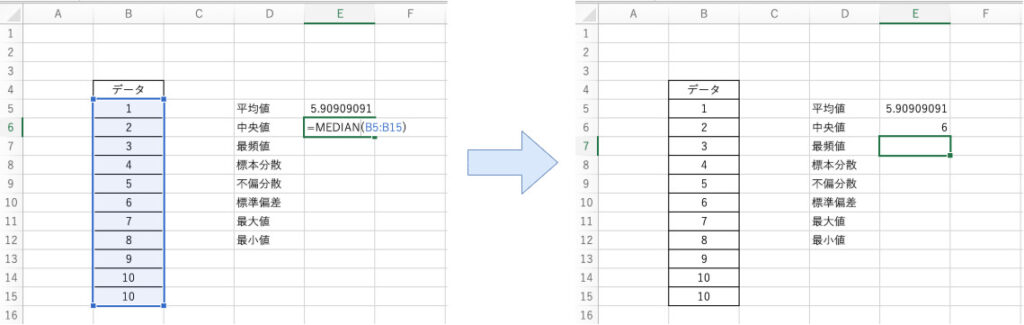
先ほどの例に対してB5~B15までのセルのデータの中央値を算出する場合、以下のように関数を適用します。
$$ \mathsf{=MEDIAN(B5:B15)} $$
以上のように関数を組み込むことで中央値を算出することができます。
関数を使った基本統計量の計算 その3:最頻値
最頻値とは、集められたデータのなかで最も多くあらわれたデータの値です。
最頻値をExcelで計算する関数は以下となります。
$$ \mathsf{=MODE(引数)} $$
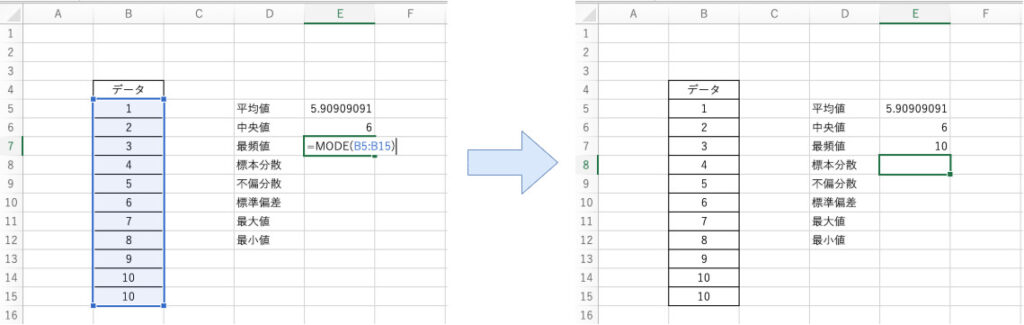
先ほどの例に対してB5~B15までのセルのデータの最頻値を算出する場合、以下のように関数を適用します。
$$ \mathsf{=MODE(B5:B15)} $$
以上のように関数を組み込むことで最頻値を算出することができます。
関数を使った基本統計量の計算 その4:標本分散
分散とは、データのばらつき具合を評価できる指標となります。
そして、標本分散は標本内のばらつき具合のことをいいます。
標本分散をExcelで計算する関数は以下となります。
$$ \mathsf{=VAR.P(引数)} $$
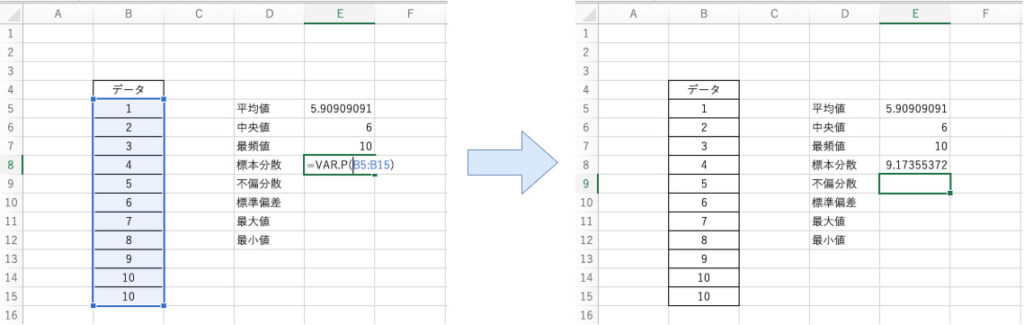
先ほどの例に対してB5~B15までのセルのデータの標本分散を算出する場合、以下のように関数を適用します。
$$ \mathsf{=VAR.P(B5:B15)} $$
以上のように関数を組み込むことで標本分散を算出することができます。
関数を使った基本統計量の計算 その5:不偏分散
不偏分散とは、標本を使って母集団のばらつきを推定した値となります。
不偏分散をExcelで計算する関数は以下となります。
$$ \mathsf{=VAR.S(引数)} $$
不偏分散と標本分散は関数の名前がよく似ているので、標本そのものの分散を計算したいのか、標本から得られる母集団の分散の推定値を計算したいのかよく吟味して関数を適用してください。
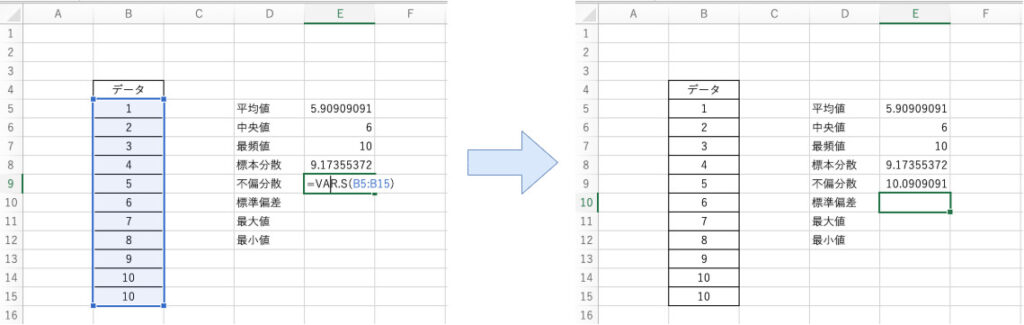
先ほどの例に対してB5~B15までのセルのデータの不偏分散を算出する場合、以下のように関数を適用します。
$$ \mathsf{=VAR.S(B5:B15)} $$
以上のように関数を組み込むことで不偏分散を算出することができます。
関数を使った基本統計量の計算 その6:標準偏差
標準偏差とは、分散の平方根をとった値のことをいいます。
分散ではばらつき具合は比較することができますが、分散を直接データや平均値等と比較することっはできません。
よって、分散の平方根をとった標準偏差を使うことで、データや平均値と比較することができるようになります。
標準偏差にも2つの種類があります。それは、標本そのものの標準偏差であるか、標本から推定される母集団の標準偏差であるかです。
標本そのものの標準偏差をExcelで計算する関数は以下となります。
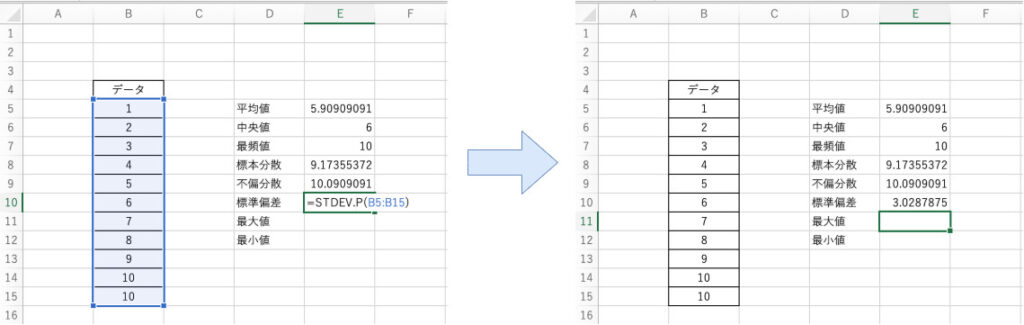
$$ \mathsf{=STDEV.P(引数)} $$
先ほどの例に対してB5~B15までのセルのデータそのものの標準偏差を算出する場合、以下のように関数を適用します。
$$ \mathsf{=STDEV.P(B5:B15)} $$
以上のように関数を組み込むことで標本そのものの標準偏差を算出することができます。
一方で、標本から推定される母集団の標準偏差をExcelで計算する関数は以下となります。
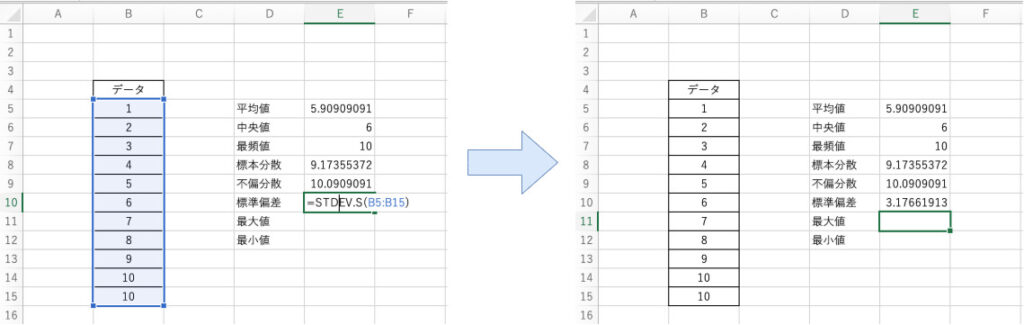
$$ \mathsf{=STDEV.S(引数)} $$
先ほどの例に対してB5~B15までのセルのデータから推定される母集団の標準偏差を算出する場合、以下のように関数を適用します。
$$ \mathsf{=STDEV.S(B5:B15)} $$
以上のように関数を組み込むことで標本から推定される母集団の標準偏差を算出することができます。
どちらの標準偏差もよく似た関数を使用して計算しますので、関数名と自分が算出したい標準偏差を確認しながら適用しましょう!
関数を使った基本統計量の計算 その7:最大値
最大値とは、データのなかで最も大きな値のことをいいます。
最大値をExcelで計算する関数は以下となります。
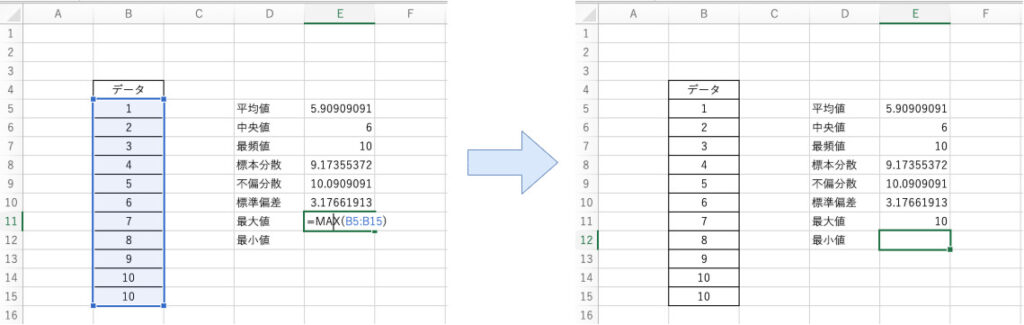
$$ \mathsf{=MAX(引数)} $$
先ほどの例に対してB5~B15までのセルのデータの最大値を算出する場合、以下のように関数を適用します。
$$ \mathsf{=MAX(B5:B15)} $$
以上のように関数を組み込むことで最大値を算出することができます。
関数を使った基本統計量の計算 その8:最小値
最小値とは、データのなかで最も小さな値のことをいいます。
最小値をExcelで計算する関数は以下となります。
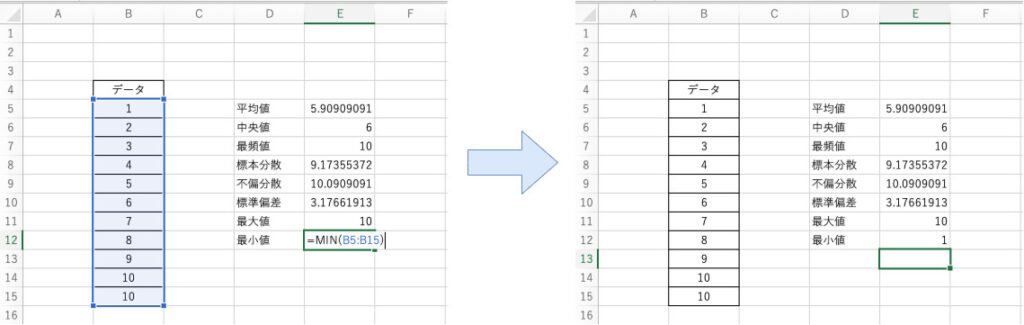
$$ \mathsf{=MIN(引数)} $$
先ほどの例に対してB5~B15までのセルのデータの最小値を算出する場合、以下のように関数を適用します。
$$ \mathsf{=MIN(B5:B15)} $$
以上のように関数を組み込むことで最小値を算出することができます。
【Excelデータ分析】Excelで基本統計量を計算する方法:まとめ
いかがでしたでしょうか?以下まとめです。
- Excelにおける関数とは、求めたい計算をかんたんに行うための機能
- Excelで関数を使うにはセル内に「=関数名(引数)」という形で適用する
- Excelの関数を使うことで、平均値・中央値・最頻値・標本分散・不偏分散・標準偏差・最大値・最小値といった基本統計量をかんたんに計算することができる
みなさんも、この記事を読んでExcelでデータ分析をすることってかんたんということを体感できたら幸いです。
Excelを使ったデータ分析方法を勉強したい方へ
Excelを使ったデータ分析をもっとよく勉強したいと思った方は「統計学の基礎から学ぶExcelデータ分析の全知識(できるビジネス) できるビジネスシリーズ」という本がおすすめです。
この本では、データ分析とはどういったものなのか、データ分析をするための心構えなどを解説しております。
そのうえで、データ分析の手法についてやその分析をExcelでどのように行えば良いかについて解説しております。
たとえば、先ほど解説したデータ分析ツールの導入方法から、基本統計量の計算方法、線形回帰モデルを作成するといった実践的なデータ分析まで網羅できる本となります。
また、各章で実践問題も組み込まれておりますので、Excelの使い方を学びつつデータ分析を実感できる本となります。
統計学を勉強したけど、具体的な実務でどうやれば良いのか、Excelでのデータ分析はどうやるのか勉強したい方に、ぜひおすすめしたい本です。
みなさんもぜひこの本を読んで、統計学を勉強したりデータ分析をExcelでできるようにしましょう!
最後までこの記事を読んでいただきありがとうございました!
【世界で37万人が受講】データサイエンティストを目指すあなたへ〜データサイエンス25時間ブートキャンプ〜




コメント