こんにちは、かじつとむです。
データを分析するのに必要なものとして仮説検定があります。
仮説検定を使えるようになると、仮説に対して現在のデータから正しいのかどうかを検証できるようになります。
しかし、具体的にどのように仮説検定をやっていけば良いかわからない人も多いはずです。
そこで今回はExcelを使って仮説検定の1つであるt検定の方法について解説します。
この記事を読むことで以下のことがわかります。
- Excelを使ったt検定の方法について理解できる
- 検定の用語であるp値について理解できる
もし仮説検定の概要を知りたい方は、こちらの記事をご参照ください!
それではいってみましょう!
Excelを使ったt検定の方法:結論

Excelを使ったt検定の方法は以下の手順で行います。
- 帰無仮説と対立仮説を設定する
- 有意水準を決める
- データの平均値・標準偏差・サンプル数を求める
- 統計量tの絶対値を計算する
- 累積確率を計算する
- p値を求める
- p値と有意水準を比較する
それぞれの手順について以下の問題を使って解説します。
ある工場で鉄の部品にピアス穴を開けている。開けているピアス穴の直径は母平均$μ=1.8$の母集団に従っている(ただし母分散は未知)。最近のピアス穴のデータを見ると穴の大きさが小さくなっているのではないかと考えたため、このときのデータは以下となる。
1.68、1.53、1.84、1.89、1.71、1.62、1.85、1.66、1.80、1.70
このとき、ピアス穴が小さくなっているか?
また、上記のデータをExcelでまとめると以下のように表せます。
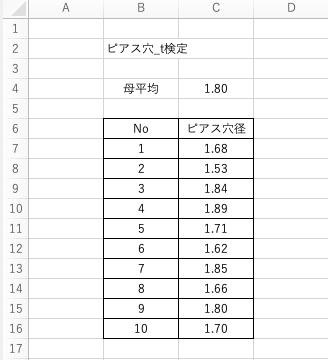
この具体例について、Excelでのt検定を手順を確認していきましょう!
Excelを使ったt検定の方法 その1:帰無仮説と対立仮説を立てる

まず帰無仮説と対立仮説を立てます。
帰無仮説とは自分が否定したい仮説です。
一方で対立仮説は自分が考えたり感じたりした仮説となります。
今回の具体例では、ピアス穴がの径が小さくなっているのではないかと感じています。
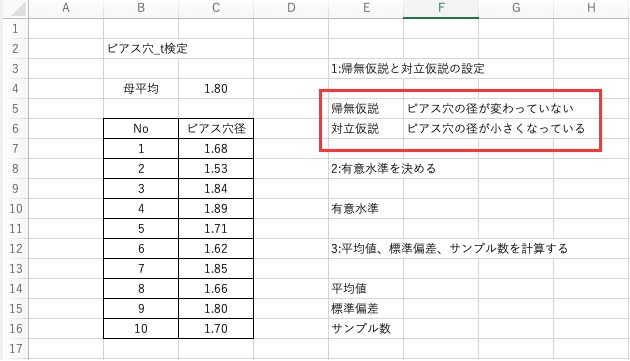
すなわち、帰無仮説と対立仮説は以下のようになります。
- 帰無仮説 $H_{0}$:ピアス穴の径が変わっていない
- 対立仮説 $H_{1}$:ピアス穴の径が小さくなっている
また、ここまでの内容をExcelでまとめると以下のようになります。
Excelを使ったt検定の方法 その2:有意水準を決める
帰無仮説と対立仮説を立てたら、有意水準を決めます。
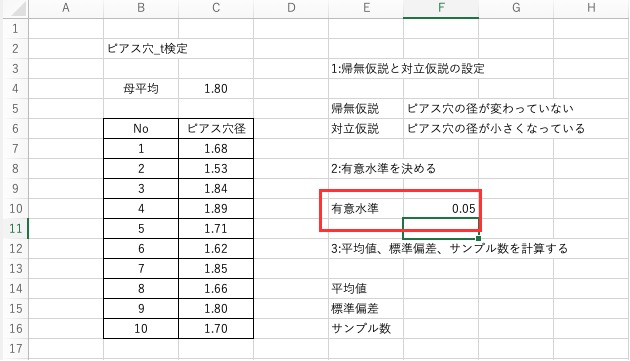
有意水準は一般的に5%か1%に設定します。
今回は有意水準を5%とします。また、Excel上では最終的にp値と比較したいため0.05と表します。
Excelを使ったt検定の方法 その3:データの平均値・標準偏差・サンプル数を求める

有意水準を決めたら次はデータの平均値・標準偏差・サンプル数を求めます。
Excelでの平均値・標準偏差・サンプル数の求め方は以下の通りになります。
$$ \mathrm{ 平均値 = AVERAGE(データ配列) } $$
$$ \mathrm{ 標準偏差 = STDEV.S(データ配列) } $$
$$ \mathrm{ サンプル数 = COUNT(データ配列) } $$
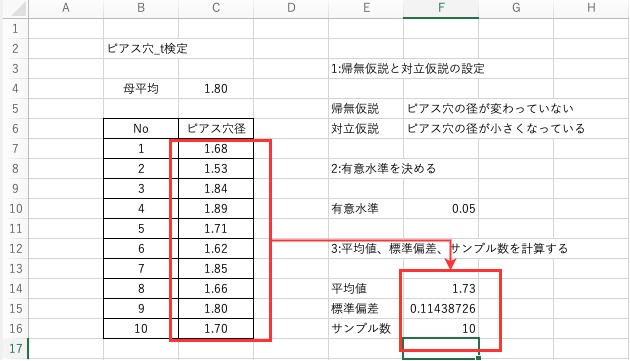
実際にExcelデータに対して当てはめると以下のようになります。
$$ \mathrm{ 平均値 = AVERAGE(C7:C16) } = 1.73 $$
$$ \mathrm{ 標準偏差 = STDEV.S(C7:C16) } \fallingdotseq 0.144 $$
$$ \mathrm{ サンプル数 = COUNT(C7:C16) } = 10 $$
Excelを使ったt検定の方法 その4:統計量tの絶対値を計算する

データの平均値・標準偏差・サンプル数を求めたら、次は統計量tの絶対値を計算します。
統計量tはt分布という正規分布のような確率分布で検定するために使われる統計量です。
この統計量tは先ほど計算したデータの平均値・標準偏差・サンプル数ともともとの母平均を使ってExcelで以下のように計算できます。
$$ \mathrm{統計量:t = \frac{(データの平均値) – (母平均)}{\frac{標準偏差}{\sqrt{サンプル数}}}} $$
実際にExcelデータで統計量tを計算すると以下のようになります。
またこのとき便宜上統計量tは絶対値として求めます。
$$ \mathrm{統計量tの絶対値 = ABS((F14 – C4)/(F15/SQRT(F16)))} \fallingdotseq 1.990 $$

Excelを使ったt検定の方法 その5:累積確率を求める

統計量tを求めたら、次は累積確率を求めます。
累積確率とは確率変数がある値以下となる確率のことをいいます。
累積確率を計算するには統計量tと自由度、そして検定が両側なのか片側なのかを使ってExcelで以下のように計算できます。
$$ \mathrm{両側検定 = 2T.DIST(統計量t, 自由度, TRUE or FALSE)} $$
$$ \mathrm{片側検定 = T.DIST(統計量t, 自由度, TRUE or FALSE)} $$
統計量tは先ほど計算で求めた値となります。
自由度は、サンプル数から1を引いた値となります。
また、t値に対して確率密度関数の値を求める場合はFALSEを、累積分布関数の値を求める場合はTRUEを指定します。
累積確率を求めるならばTRUEで良いです。
実際にExcelデータで統計量tを計算すると以下のようになります。
このとき、対立仮説として「ピアス穴が小さくなる」ということを示すために片側検定の累積確率を計算します。
$$ \mathrm{累積確率(片側)= T.DIST(J5, F16-1, TRUE)} \fallingdotseq 0.961 $$

Excelを使ったt検定の方法 その6:p値を計算する
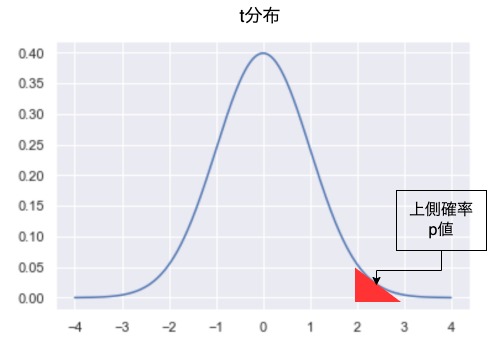
累積確率を求めたら、次はp値を計算します。
p値とは帰無仮説に対して、検定統計量の値となる確率です。
p値が小さいほど、検定統計量になる確率が小さくなります。
p値の計算は1から累積確率を引くことで計算できます。
$$ \mathrm{p値:p = 1 – (累積確率)} $$
実際にExcelデータでp値を計算すると以下のようになります。
$$ \mathrm{p値:p = 1 – J9} \fallingdotseq 0.0389 $$

Excelを使ったt検定の方法 その7:p値と有意水準を比較する
p値まで計算できたら、p値と有意水準を比較します。
有意水準に対してp値の方が大きい場合は、帰無仮説を棄却できません。
一方で、有意水準に対してp値が小さい場合、帰無仮説を棄却し対立仮説を採択できます。
今回は有意水準5%に対して、p値は0.0388となります。
よってp値の方が有意水準よりも小さいので、「ピアス穴の径が小さくなっている」という対立仮説を採択できます。
Excelを使ったt検定の方法:まとめ
いかがでしたでしょうか?以下まとめです。
- Excelを使ったt検定では、データの平均値・標準偏差・サンプル数を計算し、t値を求める
- 求めたt値を使って、累積確率を計算し、最終的にp値を求める
- p値と有意水準を比較し、帰無仮説が棄却できるかどうか判断する
みなさんもぜひExcelを使った検定についてやってみてください!
Excelを使った統計学を学びたい方へ

Excelを使った統計学を勉強したい方は「統計学の基礎から学ぶ Excelデータ分析の全知識 (できるビジネス)」がおすすめです。
この本では、データ分析とはどういったものなのか、データ分析をするための心構えなどを解説しております。
そのうえで、データ分析の手法についてやデータをさまざまなグラフで作成する方法についても解説しております。
たとえば、データ分析ツールの導入方法から、データ分析ツールとを使った基本統計量の計算方法、先ほど紹介した散布図などのグラフの作成、さらには線形回帰モデルを作成するといった実践的なデータ分析まで網羅できる本となります。
また、各章で実践問題も組み込まれておりますので、Excelの使い方を学びつつデータ分析を実感できる本となります。
統計学を勉強したけど、具体的な実務でどうやれば良いのか、Excelでのデータ分析はどうやるのか勉強したい方に、ぜひおすすめしたい本です。
みなさんもぜひExcelでのデータ分析の知識を学んでビジネスに役立てましょう!
最後までこの記事を読んでいただきありがとうございました!
統計学・機械学習を動画で学ぶなら「【世界で37万人が受講】データサイエンティストを目指すあなたへ〜データサイエンス25時間ブートキャンプ〜」がおすすめ!





コメント