こんにちは、かじつとむです。
前回は機械学習に必要な数学について解説しました。
今回は機械学習に欠かせない数学の1つである微分について解説します。
機械学習のモデルを構築するのに必ず関わってくるのが微分です。
そんな微分について、意味から計算方法、機械学習にどのように適用されているかまでを説明します。
この記事を読むことで以下のことがわかります。
- 微分の意味や計算方法について理解できる
- 機械学習での微分の使われ方について理解できる
それではいってみましょう!
機械学習で使う微分とは
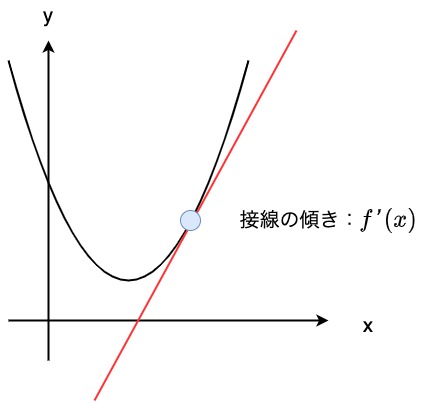
微分とはある関数の接線の傾きを計算する手法です。
関数の接線の傾きがわかると何ができるのでしょうか?
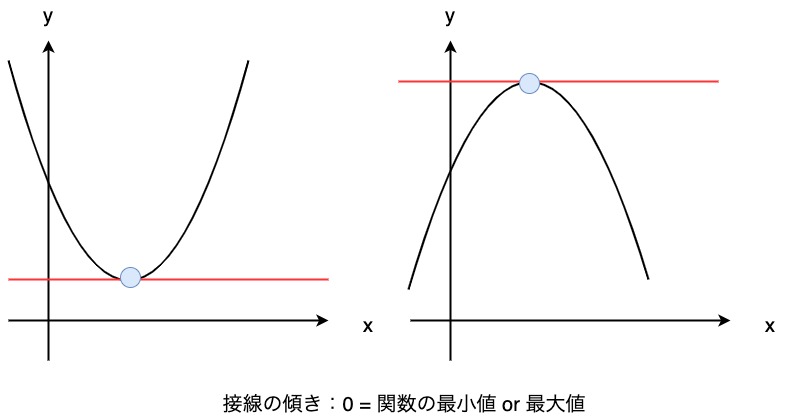
答えは、接線の傾きが0であることで関数の最小値(もしくは最大値)となる点を求めることができることです。
機械学習では実測値とあらかじめ定義した数式で得られる予測値の差の関数を考えます。
この関数を損失関数といいます。
損失関数がもっとも小さくなる予測値の数式のパラメータを求めることで機械学習のモデルを構築します。
このときに各パラメータ毎に微分し、0となる値が最も予測精度の良い数式のパラメータとなります。
要するに微分による傾き0を利用することで、機械学習モデルを構築しているのです。
微分の意味や機械学習での使われ方がわかったところで、次は微分の計算方法について解説します。
微分の計算方法
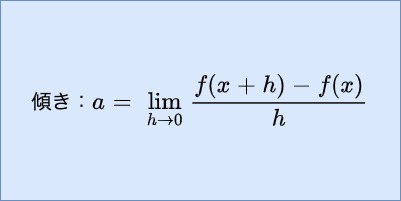
では実際に微分を計算していきましょう!
まずは関数$f(x)$に対する2点間の直線$y = ax + b$を考えていきましょう。
このときの2点は$(x_{1}, f(x_{1}))$、$(x_{2}, f(x_{2}))$とします。
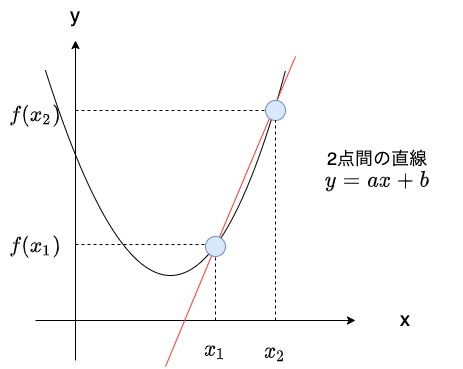
すると、2点間の直線の傾き$a$は以下のように計算することができます。
$$ \begin{eqnarray}
傾き:a &=& \frac{f(x)の増加量}{xの増加量} \\
&=& \frac{f(x_{2}) – f(x_{1})}{x_{2} – x_{1}} \\
\end{eqnarray} $$
これで2点間の直線の傾きを求めることができます。
では関数に対して1点、すなわち接線の傾きを計算するにはどうすれば良いのでしょうか?
答えは先ほどの$x_{2}$を$x_{1}$に限りなく近づけることで接線の傾きを計算することができるようになります。
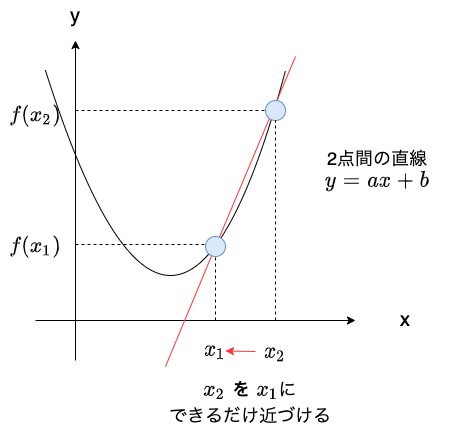
具体的な計算方法として、まず便宜上$x_{1}$を$x$、$x_{2}$を$x + h$とします。
すると2点間の傾きは以下のようにあらわすことができます。
$$ \begin{eqnarray}
傾き:a &=& \frac{f(x + h) – f(x)}{(x + h) – x} \\
&=& \frac{f(x + h) – f(x)}{h}
\end{eqnarray} $$
ここで$x + h$を$x$に近づけるには$h$が限りなく0となるようにすれば良いということになります。
ここで使われるのが極限の考え方です。

極限とは対象に対して、変数がある値に限りなく近づくという意味です。
上記の画像では、$f(x)$という対象に対して$x$が3に限りなく近づくという意味です。
接線の傾きを計算するには$x + h$にある$h$を限りなく0に近づければ良いということがわかります。
よって接線の傾き$a$は以下のように計算することができます。
$$ 傾き:a = \lim_{h \to 0} \frac{f(x + h) – f(x)}{h} $$
これが接線の傾きであり、微分の計算方法になります。
では具体的に計算をしてみましょう!
関数を$f(x) = x^2$と考えると接線の傾きは以下のようになります。
$$ \begin{eqnarray}
傾き:a &=& \lim_{h \to 0} \frac{(x + h)^2 – x^2}{h} \\
&=& \lim_{h \to 0} \frac{x^2 + 2xh + h^2 – x^2}{h} \\
&=& \lim_{h \to 0} (2x + h) \\
&=& 2x
\end{eqnarray} $$
以上より、$f(x) = x^2$の接線の傾きは$2x$であることがわかりました。
計算するときの注意点は、まず対象となる部分を計算してから、変数に値を代入するということです。
こうしないと、うまく値が計算できませんので必ず対象の計算→変数に値の代入の順番で計算しましょう!
微分の記号と公式

定義としての微分がわかったところで、微分の記号と公式について説明します。
まず。微分の記号ですが$\frac{df(x)}{dx}$もしくは$f'(x)$であらわします。
$\frac{df(x)}{dx}$はライプニッツの記法といい、「ディーエフエックスディーエックス」と呼びます。
$f'(x)$はラグランジュの記法といい、「エフエックスプライム」と呼びます。
次に微分の公式について説明します。
微分は先ほどの定義通りに計算すれば良いのですが、とても手間がかかります。
そこで計算が楽になるよう代表的な微分の公式を2つだけ紹介します。
なおこれ以外にも三角関数や対数関数といった特殊な関数については別途解説します。

一般的な関数の微分は、$x$に対してその次数である$n$を係数としておろし、元々の次数を1減らした関数となります。
また定数の微分は次数となる$n$が0であるため、係数が0となり、どんな定数であっても0となります。
これだけ覚えていれば基本的な関数に対する微分はできます。
では具体例を用いて微分をしてみましょう!
今回用いる関数は$f(x) = 2x^2 + 4x + 16$とすると、その微分は以下のように計算します。
$$ \begin{eqnarray}
\frac{df(x)}{dx} &=& (2x^2 + 4x + 16)’ \\
&=& (2x^2)’ + (4x)’ + (16)’ \\
&=& 2(x^2)’ + 4(x)’ + 16(1)’ \\
&=& 2 \times 2x + 4 \times 1 + 16 \times 0 \\
&=& 4x + 4
\end{eqnarray} $$
以上のように関数の微分を公式を用いて行うことができます。
微分のコツは微分の対象となる変数の次数ごとにわけて微分の公式を適用することです。
次数ごとわけることで、計算過程を微分を適用しているものなのか他の計算なのかを分けて考えることができるためです。
以上、微分の記号と公式についてでした。
機械学習で使う微分とは:まとめ
いかがでしたでしょうか?以下まとめです。
- 微分とは、関数の接線の傾きを計算する方法
- 微分は関数の最小値(もしくは最大値)となる点を求めることができる
- 機械学習では損失関数の最小値を計算することで、予測モデルのパラメータの値を決める。その際、微分が使用される
- 微分は2点間の関数の増加量を変数の増加量で割った傾きを求め、その2点間を限りなく近づけることで計算する
みなさんも機械学習を勉強するならば、ぜひ微分の知識を身につけていきましょう!
微分と機械学習についてもっと勉強したい方へ
微分と機械学習についてもっと勉強したい方はUdemyの講座「【キカガク流】人工知能・機械学習 脱ブラックボックス講座 – 初級編 –」がおすすめです。
この講座では、機械学習やAIの概要から機械学習の1番単純なモデルである単回帰分析をPythonで実装するところまでを教えてくれます。
概要はもちろんのこと、機械学習に必要な数学の概要からその一部である微分についてもしっかり学ぶことができます。
この講座の面白いところはパワーポイントではなく手書きで教えてくれるという点です。
自分でも手書きをしながら回帰分析のメカニズムを勉強することができます。
機械学習に興味を持っていて、数学をあまり勉強していかなかった人やプログラミング初心者の方に超おすすめの講座となっています。

ぜひこの機会に機械学習について少し勉強してみてはいかがでしょうか?
最後までこの記事を読んでいただきありがとうございます。
機械学習以外にも新しいスキルを動画で学びたい方はUdemyがおすすめ!




コメント